Analyse Séquentielle Sociale
Chargement des packages
library(tidyverse)
library(kableExtra)
library(TraMineR)
library(TraMineRextras)
library(cluster)
library(WeightedCluster)
library(seqhandbook)Introduction
Les enquêtes socio-démographiques permettent de collecter des informations permettant de retracer le parcours des individus, en considérant le parcours d’un individu comme une séquence(une suite d’états ou d’événements dans un espace fini de modalités). Ainsi, on pourra étudier les trajectoires des individus en définissant l’appartenance de chaque individu à chaque âge à un état (étude, formation universitaire, formation continue, emploi, chômage …) et de répondre à des questions telles que:
- Les parcours de vie obéissent-ils à une norme sociale?
- Quelles sont les types de trajectoires standards?
- Quels écarts observe-t-on par rapport à ces normes?
- Pourquoi certaines personnes suivent-elles des trajectoires plus chaotiques que d’autres?
- Comment les trajectoires de vie sont-elles liées au sexe, à l’origine sociale et à d’autres facteurs?
- Existe-t-il des règles séquentielles entre les états?
Dans ce tutoriel, nous allons voir un exemple d’analyse séquentielle avec le packages TraMineR disponible sous R. Ce package propose un certain nombre de graphiques permettant de visualiser les trajectoires les plus fréquentes ou hétérogènes ; utilisations de divers méthodes notamment optimal matching (Robette and Thibault 2008) pour une classification afin de regrouper des trajectoires en classes.
Description des données
Les données utilisées dans ce tutoriel sont celles associées au packages et proviennent d’une enquête de McVicar et Anyadike-Danes (2002) auprès de 712 jeunes irlandais sur la transition entre formation et emploi entre septembre 1993 et juin 1999. Les séquences représentent leur suivi pendant les 6 années suivant la fin de la scolarité obligatoire (16 ans) et sont constituées de 70 variables indiquant les états mensuels successifs de chaque individu.
Les états sont :
- EM : en emploi
- FE : formation continue
- HE : formation supérieure
- JL : au chômage ou inactivité
- SC : Ecole
- TR : en stage ou apprentissage.
Les données contiennent également d’autres variables catégorielles comme :
- id : numéro d’identification
- male : le sexe
- catholic : catholique ou non
- Belfast, N.Eastern, Southern, S.Eastern, Western : emplacement de l’ école.
- funemp : situation professionnelle du père au moment de l’enquête, 1 = père au chômage
- livboth : conditions de vie au moment du premier balayage de l’enquête (juin 1995), 1 = vivant avec les deux parents.
Chargement et préparation des données
Nous commençons par charger les données mvad, on vérifie les états disponibles et ensuite, nous créons un objet de séquence d’états auquel nous attribuons, pour une utilisation ultérieure, des noms d’état courts pour la sortie imprimée et des étiquettes d’état longues pour la légende dans les graphiques.
data(mvad)
seqstatl(mvad[, 17:86])## [1] "employment" "FE" "HE" "joblessness" "school"
## [6] "training"mvad.scodes <- c("EM", "FE", "HE", "JL", "SC", "TR")
mvad.labs <- c("emploi", "formation continue", "formation supérieure", "inactivité", "Ecole", "stage")
mvad.seq <- seqdef(mvad, 17:86, states = mvad.scodes, labels = mvad.labs, xtstep = 6)Déterminons le nombre de séquences distinctes dans notre corpus.
seqtab(mvad.seq, idxs = 0) %>% nrow## [1] 490Notre corpus de 712 séquences comporte 490 séquences distinctes, il est donc important d’utiliser une procédure statistique pour regrouper les séquences qui se ressemblent afin de faciliter l’analyse.
# Le chronogramme
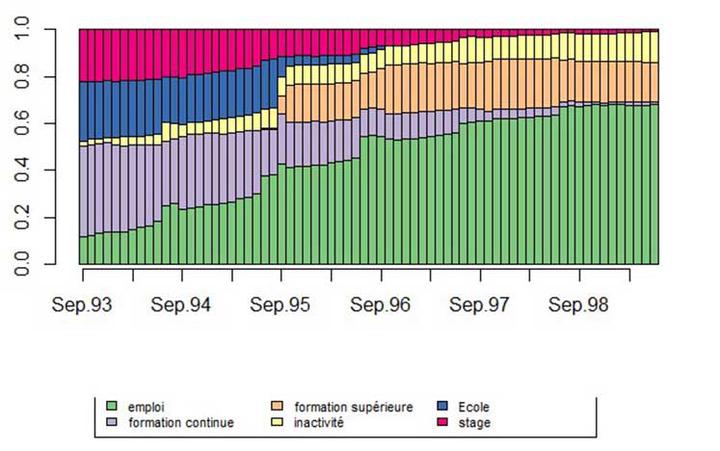
seqdplot(mvad.seq, cex.legend = 1.5)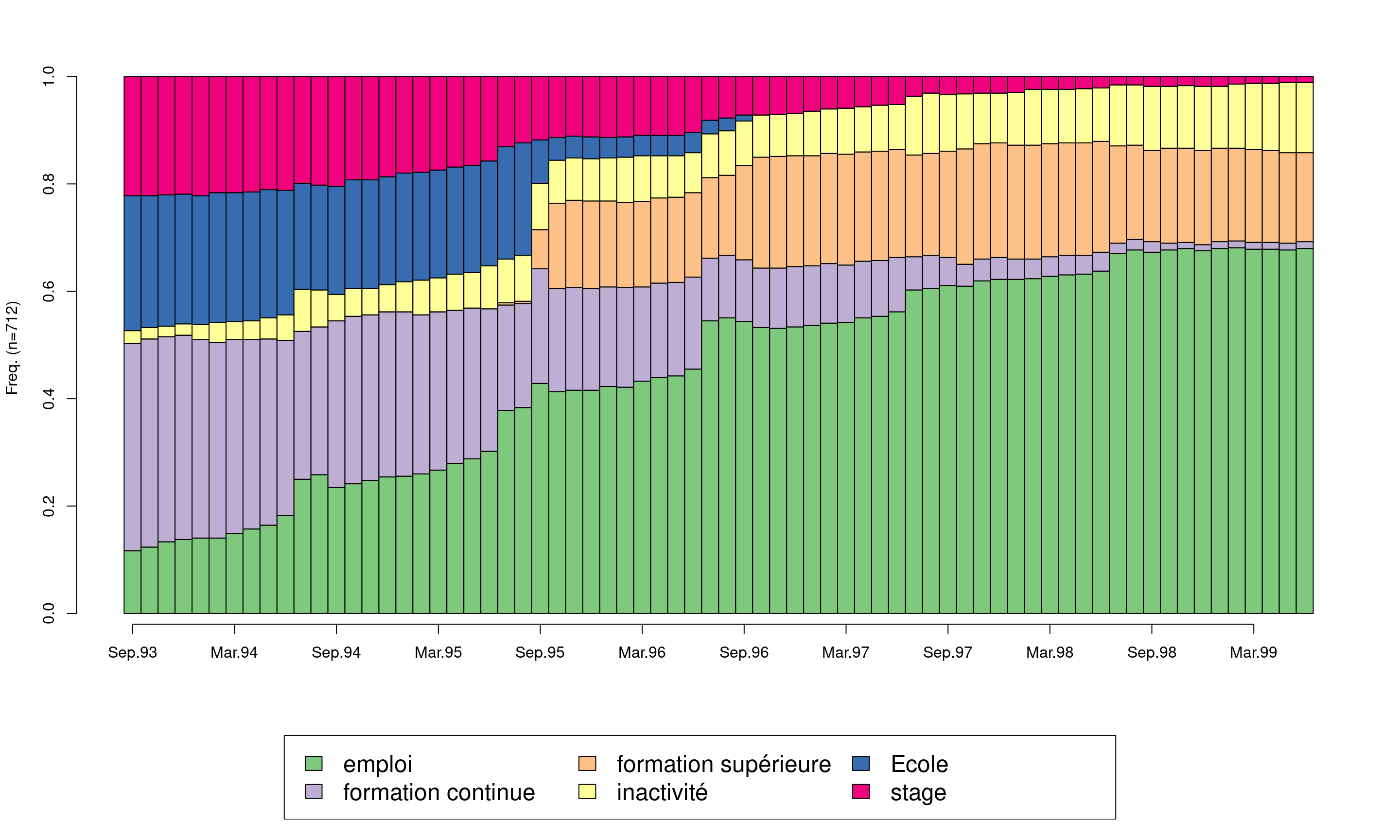
Le chronogramme (state distribution plot) de l’ensemble des séquences fait apparaître la prépondérance de l’emploi et le poids non négligeable de l’inactivité et de la formation supérieure.
Appariement optimal et classification
Calculons la dissimilarités entre les paires de séquences afin de pouvoir comparer les séquences. Notons qu’il exite plusieurs méthodes, mais ici nous optons pour la méthode la plus répandue qui est celle de l’appariement optimal (optimal matching en anglais). Pour plus de détails sur le choix des méthodes du calcul de la dissimilarités, veuillez consulter (Studer and Ritschard 2016). La méthode d’appariement optimal repose sur le nombre minimal de modifications (substitutions, suppressions, insertions) nécessaire pour obtenir une paire de séquences semblable. On peut considérer que chaque modification est équivalente, mais il est aussi possible de prendre en compte le fait que les distances entre les différents états n’ont pas toutes la même «valeur» (par exemple, on peut supposer logiquement que la distance sociale entre école et emploi est plus grande que la distance entre stage et emploi), en assignant aux différentes modifications des « coûts » distincts.
Dans notre cas, nous allons Calculer des dissimilarités OM avec la fonction seqdist entre paires de séquences avec un coût d’indel (insertions, suppressions) de 1 et des coûts de substitutions constats et égaux à 2.
couts <- seqsubm(mvad.seq, method = "CONSTANT", cval = 2)
mvad.dist <- seqdist(mvad.seq, method = "OM", indel = 1, sm = couts)La matrice des distances étant calculée, regroupons les séquences en classes en fonction de leur proximité par une classification ascendante hiérarchique (CAH) avec la fonction agnes du package cluster.
mvad.class <- agnes(as.dist(mvad.dist), method = "ward", keep.diss = FALSE)Commençons par explorer le dendrogrammme de notre CAH pour le choix du nombre de classe.
plot(as.dendrogram(mvad.class) , leaflab = "none")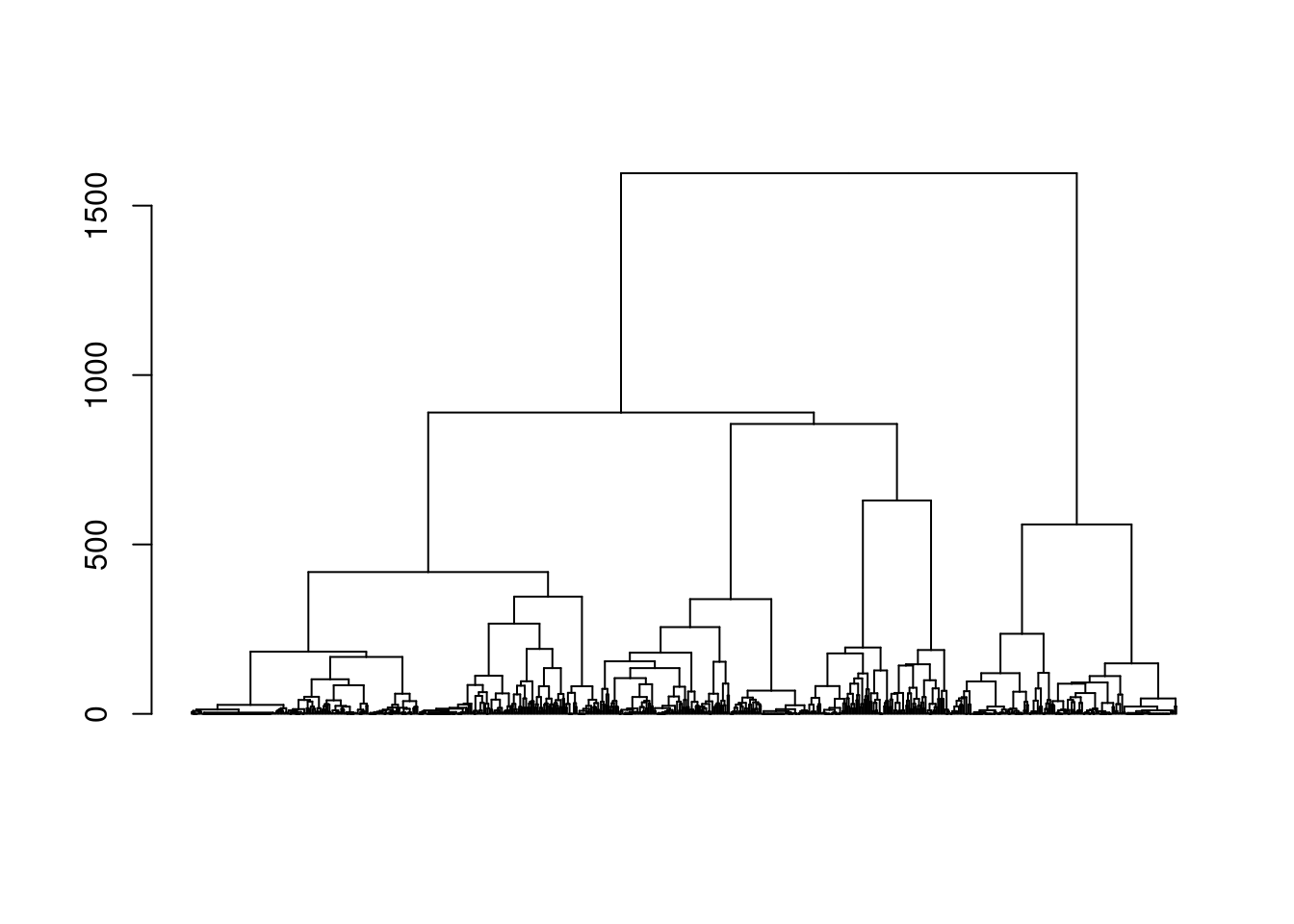
Le dendrogramme suggère une solution à 2, 4, 6 … classes. Le graphique suivant permet de représenter le tapis de l’ensemble des séquences selon l’ordre du dendrogramme.
seq_heatmap(mvad.seq, mvad.class)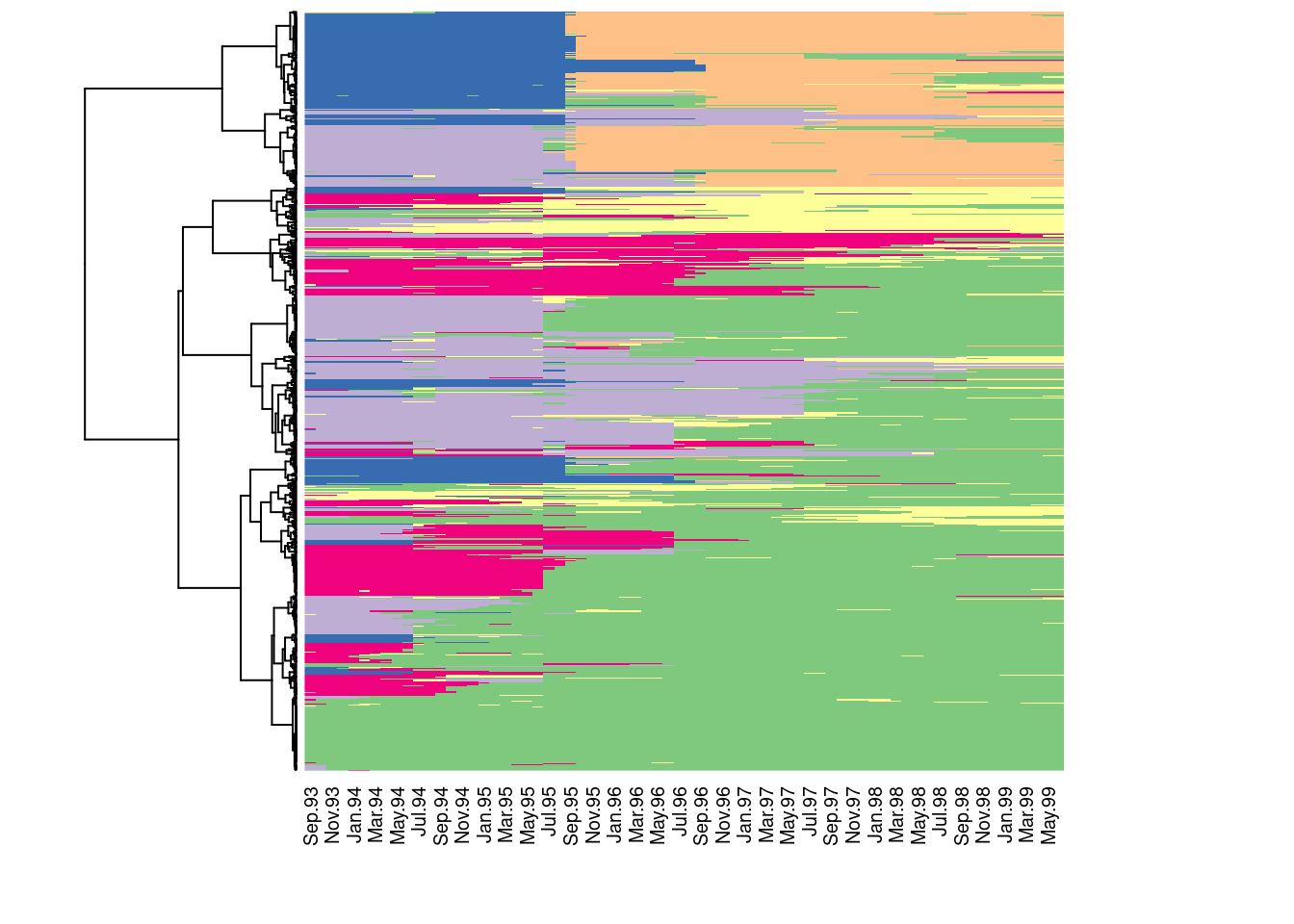
Examinons les sauts d’inertie qui peuvent être utile pour la détermination du nombre de classes.
plot(sort(mvad.class$height, decreasing = TRUE)[1:15], type="s", xlab="nombre de classes", ylab = "inertie")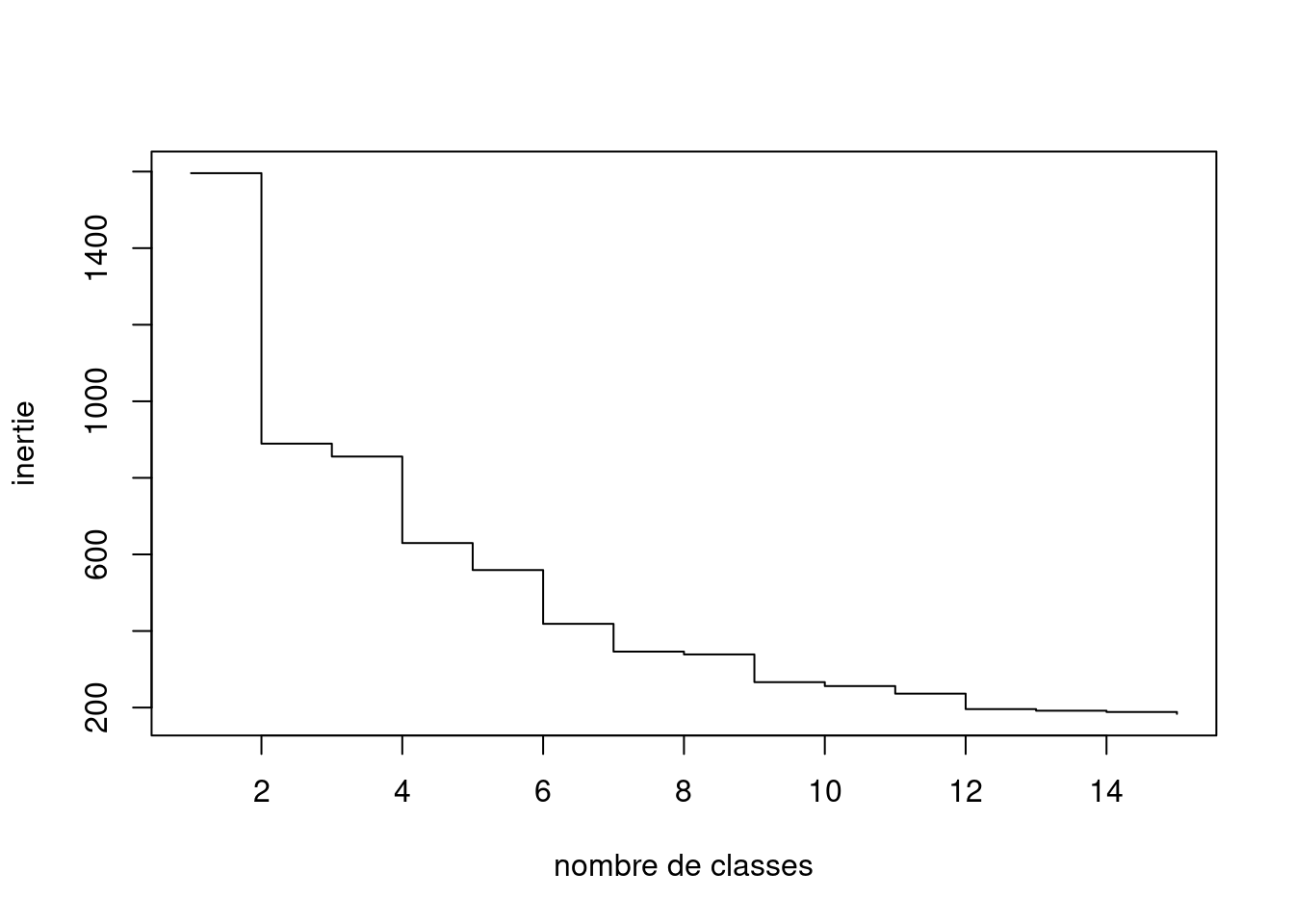
On voit par exemple qu’il y a une différence d’inertie notable entre les partitions en 5 et 6 classes.
Pour le choix d’une partition, il existe aussi un certain nombre d’indicateurs de qualité des partitions : PBC (Point Biserial Correlation), HG (Hubert’s Gamma), HGSD (Hubert’s Somers D), ASW (Average Silhouette Width), etc… Veuillez consulter (Studer 2013) pour les détails sur les indicateurs. Pour calculer ces indicateurs, on utilise la fonction as.clustrange du package WeightedCluster. L’argument max.rank spécifie le nombre de partitions à afficher par indicateur.
mvad.meas <- as.clustrange(mvad.class, diss = mvad.dist)
summary(mvad.meas, max.rank = 2)## 1. N groups 1. stat 2. N groups 2. stat
## PBC 5 0.66651242 6 0.6634702
## HG 15 0.93480644 14 0.9306607
## HGSD 15 0.93181610 14 0.9276032
## ASW 2 0.44659598 6 0.3979976
## ASWw 2 0.44801622 6 0.4028625
## CH 2 233.90963533 3 190.7425626
## R2 20 0.71651673 19 0.7119099
## CHsq 2 481.43473169 6 442.9024898
## R2sq 20 0.89524035 19 0.8914187
## HC 15 0.04732268 14 0.0494128Il est souvent utile d’observer l’évolution des ces mesures pour identifier les partitions qui offrent
le meilleur compris entre plusieurs identificateurs. La fonction plot associée à l’objet retourné par
as.clustrange représente graphiquement cette évolution.
plot(mvad.meas, stat=c("ASWw", "HG", "PBC"), norm="zscore")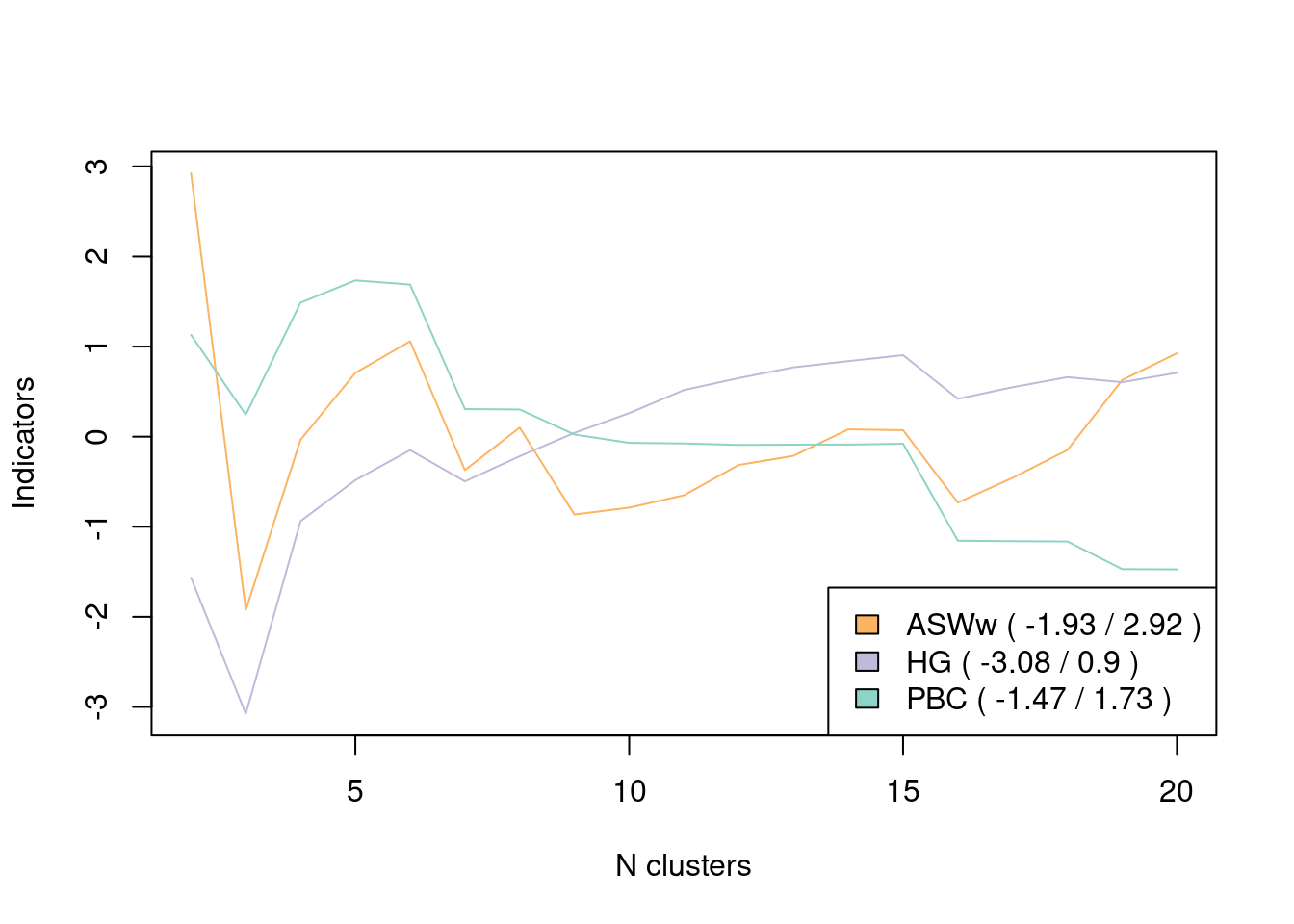
La solution en six groupes est ici un maximum local pour les mesures “ASWw”,
“PBC” et “HG”. On opte finalement pour une solution en six classes. On coupe donc l’arbre de la CAH à l’aide de la fonction cutree.
nbcl <- 6
mvad.cut <- cutree(mvad.class, nbcl)
mvad.cut <- factor(mvad.cut, labels = paste("classe", 1:nbcl, sep = " "))Représentations graphiques
Les représentations graphiques permettent de se faire une première idée sur la nature des classes de la typologie. Le type de graphique le plus utilisé est le chronogramme (state distribution plot) présentant une série de coupes transversales. Ce graphique s’obtient avec seqdplot:
seqdplot(mvad.seq, group = mvad.cut, border = TRUE, cex.legend = 2)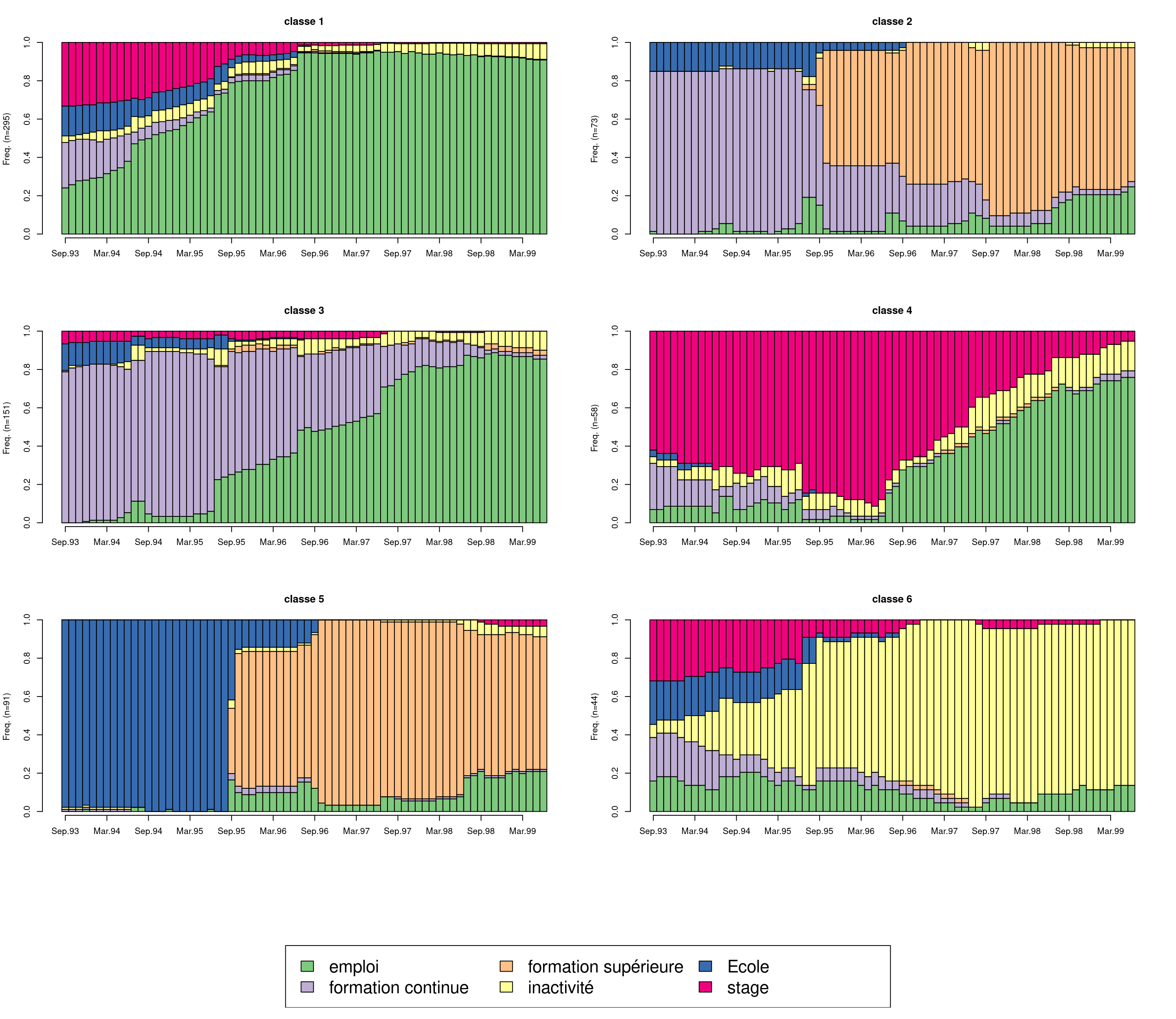
On remarque que les classes semblent caractérisées par des groupes d’états bien identifiés : emploi pour la classe 1, une formation supérieur après une formation continue pour la classe 2, emploi après une formation continue pour la classe 3. stage pour la classe 4, formation supérieur après école pour la classe 5 et chômage pour la classe 6.
Les index plots (ou “tapis”) sont également très utiles permettant de mieux visualiser la dimension individuelle des séquences. Chaque segment horizontal représente une séquence, découpée en sous-segments correspondant aux différents états successifs qui composent la séquence.
ordre <- cmdscale(as.dist(mvad.dist), k = 1)
seqiplot(mvad.seq, group = mvad.cut, sortv = ordre, idxs = 0, space = 0,
border = NA, with.legend = T, yaxis = FALSE, cex.legend = 2)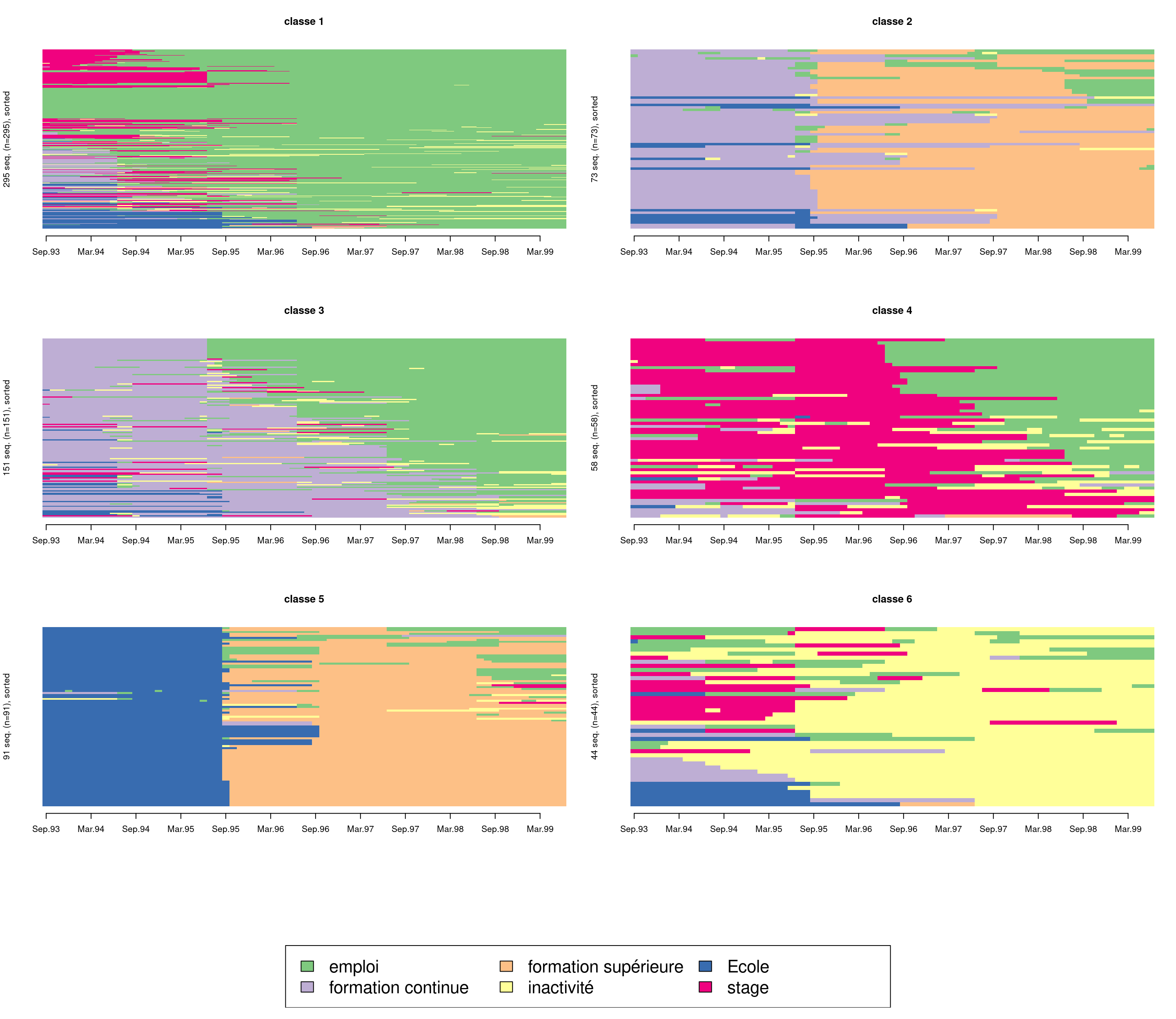
L’hétérogénéité de certaines classes se fait distinguée. Par exemple, les classes 1, 6 semblent regrouper des carrières relativement stables (respectivement employés et chômeurs) et des classes mobiles, par exemple les classes 2, 3 regroupent les individus qui ont commencé avec une formation continue et poursuivre respectivement avec une formation supérieure et un emploi. De même, la classe 4 regroupe les individus qui ont trouvé un emploi après avoir finir leur stage.
aggregate(disscenter(as.dist(mvad.dist), group = mvad.cut), list(mvad.cut), mean)## Group.1 x
## 1 classe 1 20.60026
## 2 classe 2 17.81985
## 3 classe 3 22.19771
## 4 classe 4 24.33591
## 5 classe 5 12.27726
## 6 classe 6 25.63430Cela confirme que les classes 1, 6 sont les plus hétérogènes, alors que la classe 5 est la plus homogène.
On peut visualiser les 10 séquences les plus fréquentes de chaque classe avec la fonction seqfplot
seqfplot(mvad.seq, group = mvad.cut, with.legend = T, yaxis = FALSE, cex.legend = 2)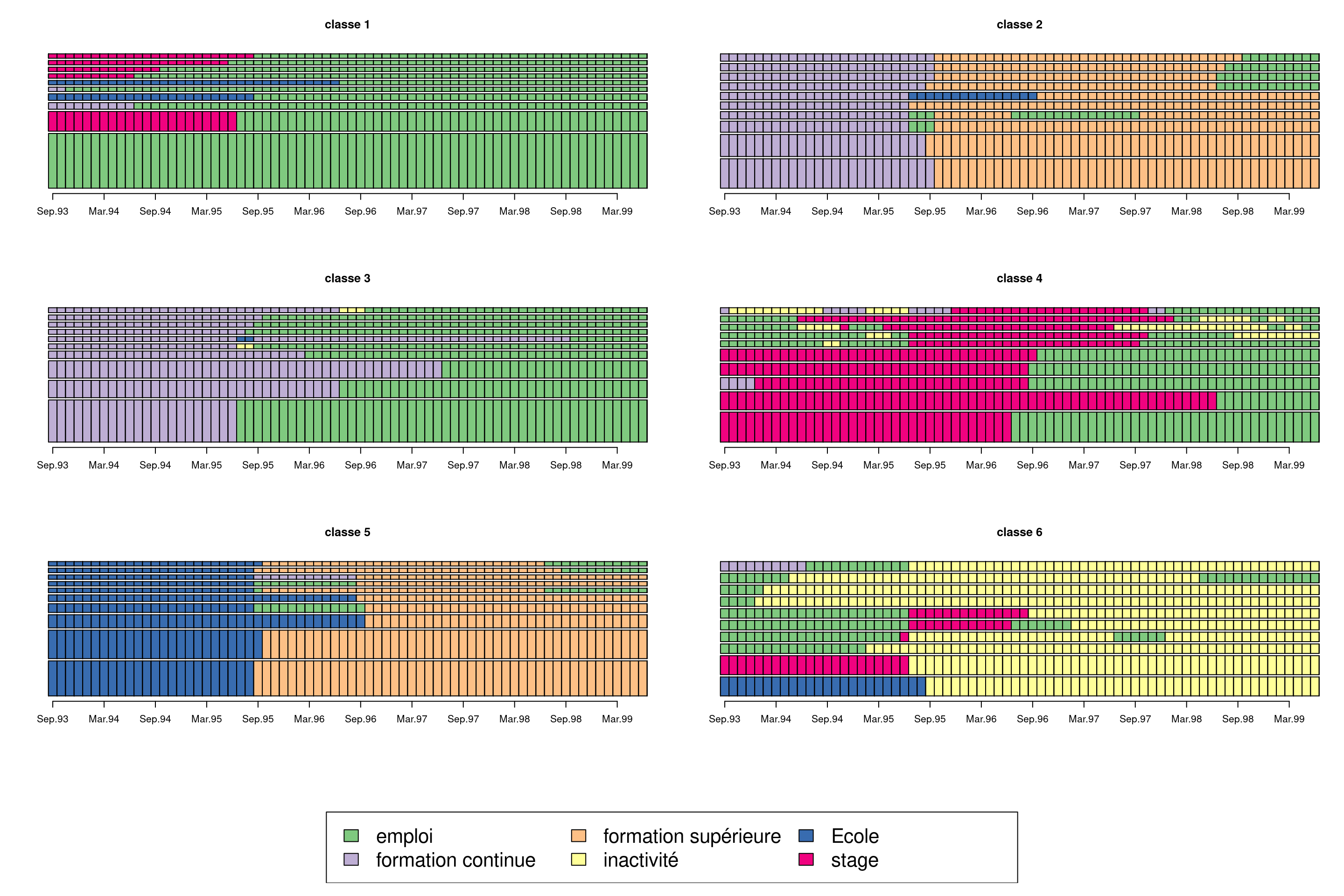
On peut aussi visualiser avec seqmsplot l’état modal (celui qui correspond au plus grand nombre de séquences de la classe).
seqmsplot(mvad.seq, group = mvad.cut, main = "classe", cex.legend = 2)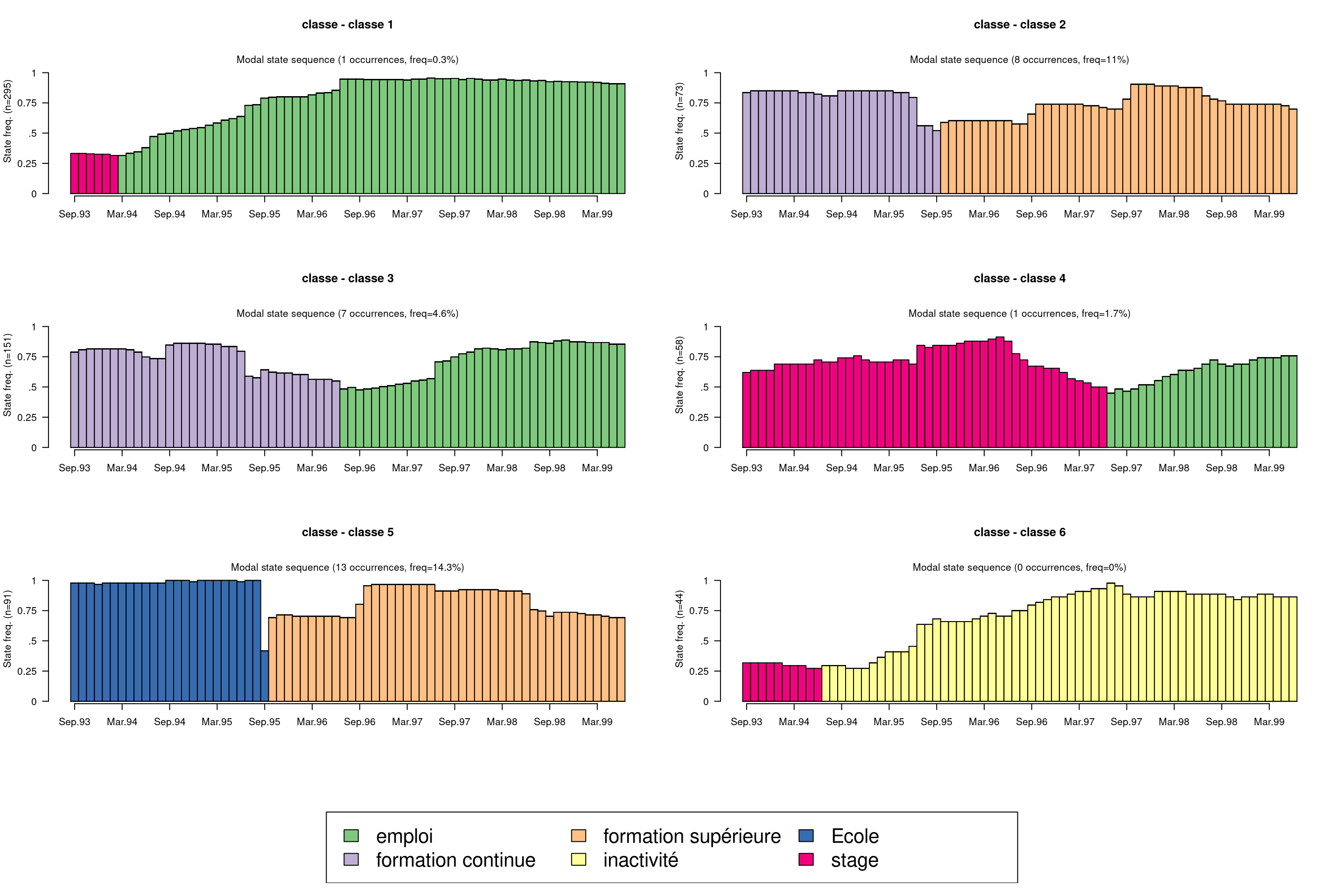
On peut également représenter avec seqmtplot les durées moyennes passées dans les différents états.
seqmtplot(mvad.seq, group = mvad.cut, cex.legend = 2)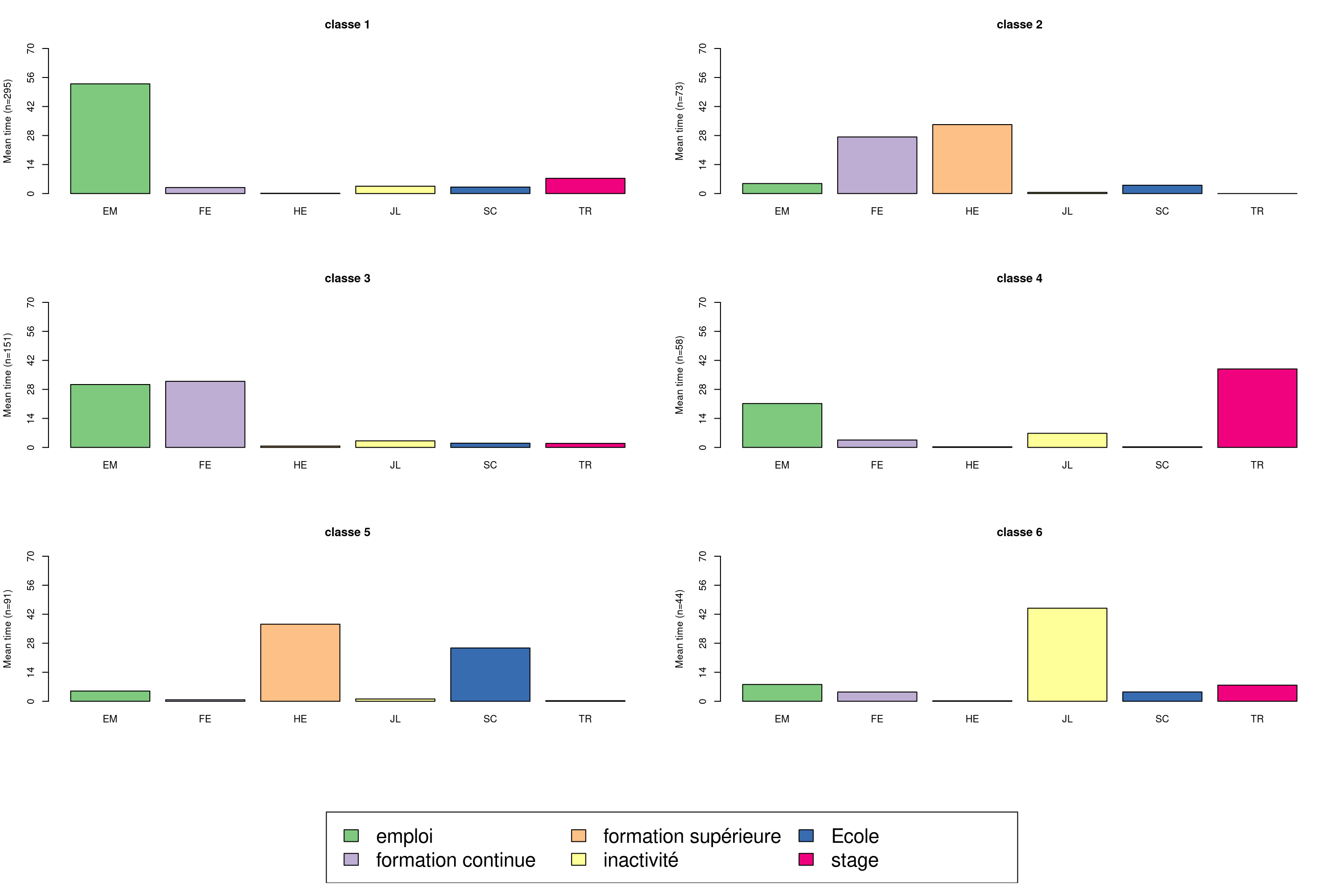
Il est également possible d’identifier des séquences représentatives de chaque classe.
seqrplot(mvad.seq, group = mvad.cut, dist.matrix = mvad.dist, criterion = "dist", cex.legend = 2)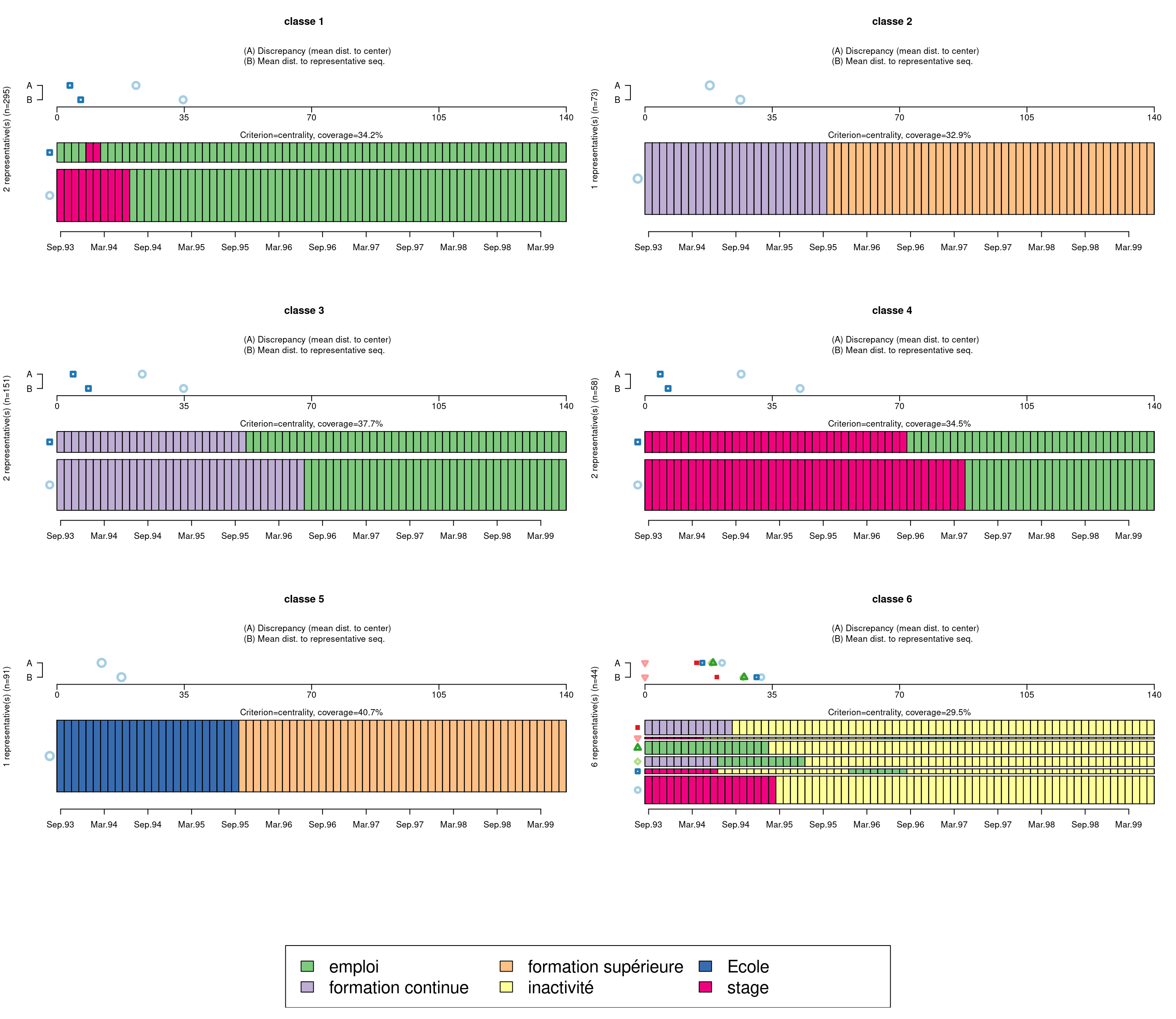
L’entropie transervale
L’entropie transversale décrit l’évolution de l’homogénéité de la classe. Pour un instant donné, une entropie proche de 0 signifie que tous les individus de la classe (ou presque) sont dans la même situation. A l’inverse, une entropie proche de 1 signifie des individus sont dispersés dans toutes les situations. Ce type de graphique est pratique pour localiser les moments de transition.
seqHtplot(mvad.seq, group = mvad.cut)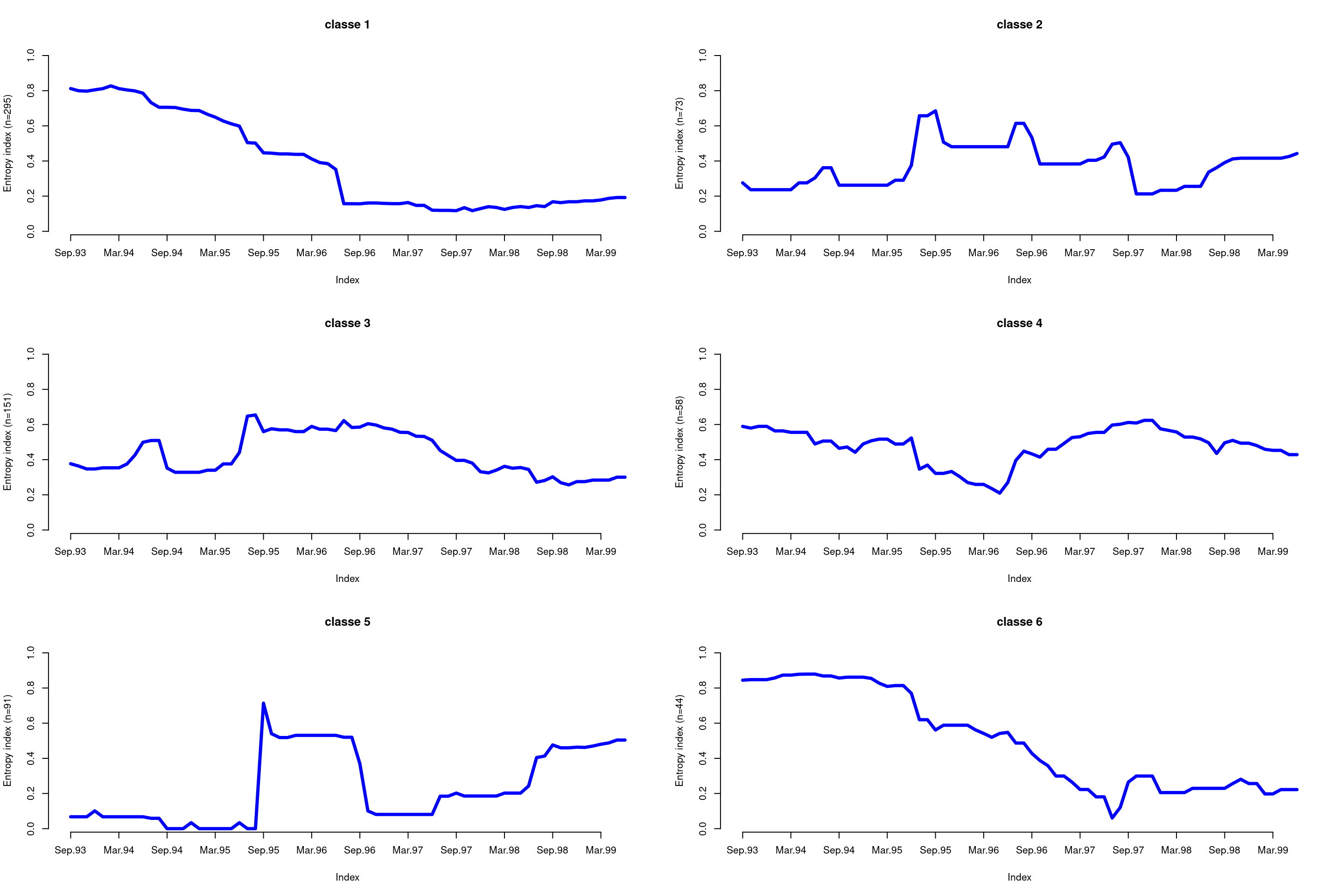
Remarque : Les mêmes analyses sont possibles en considérant les variables catégorielles (male, funemp , livboth , etc.. ) à la place des classes précédemment formées. Prenons par exemple le cas de la variable Male:
seqdplot(mvad.seq, group = mvad$male, border = TRUE, cex.legend = 1.5)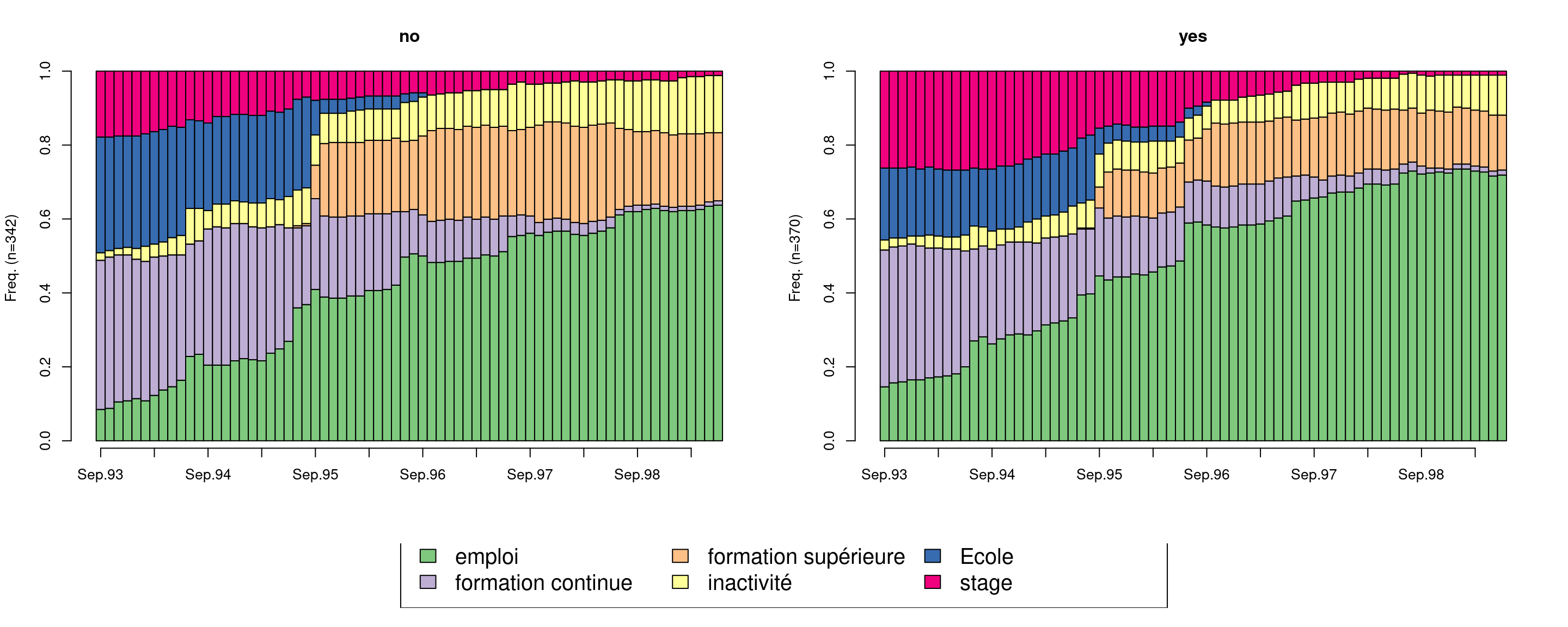
Le chronogramme (state distribution plot) de l’ensemble des séquences au niveau des deux sexes fait apparaître la prépondérance de l’emploi mais un taux élevé chez les hommes plus que chez les femmes. Les femmes ont une tendance plus forte à faire une formation continue que les hommes.
Visualisons les 10 séquences les plus fréquentes niveau de chaque sexe
seqfplot(mvad.seq, group = mvad$male, with.legend = T, yaxis = FALSE, cex.legend = 2)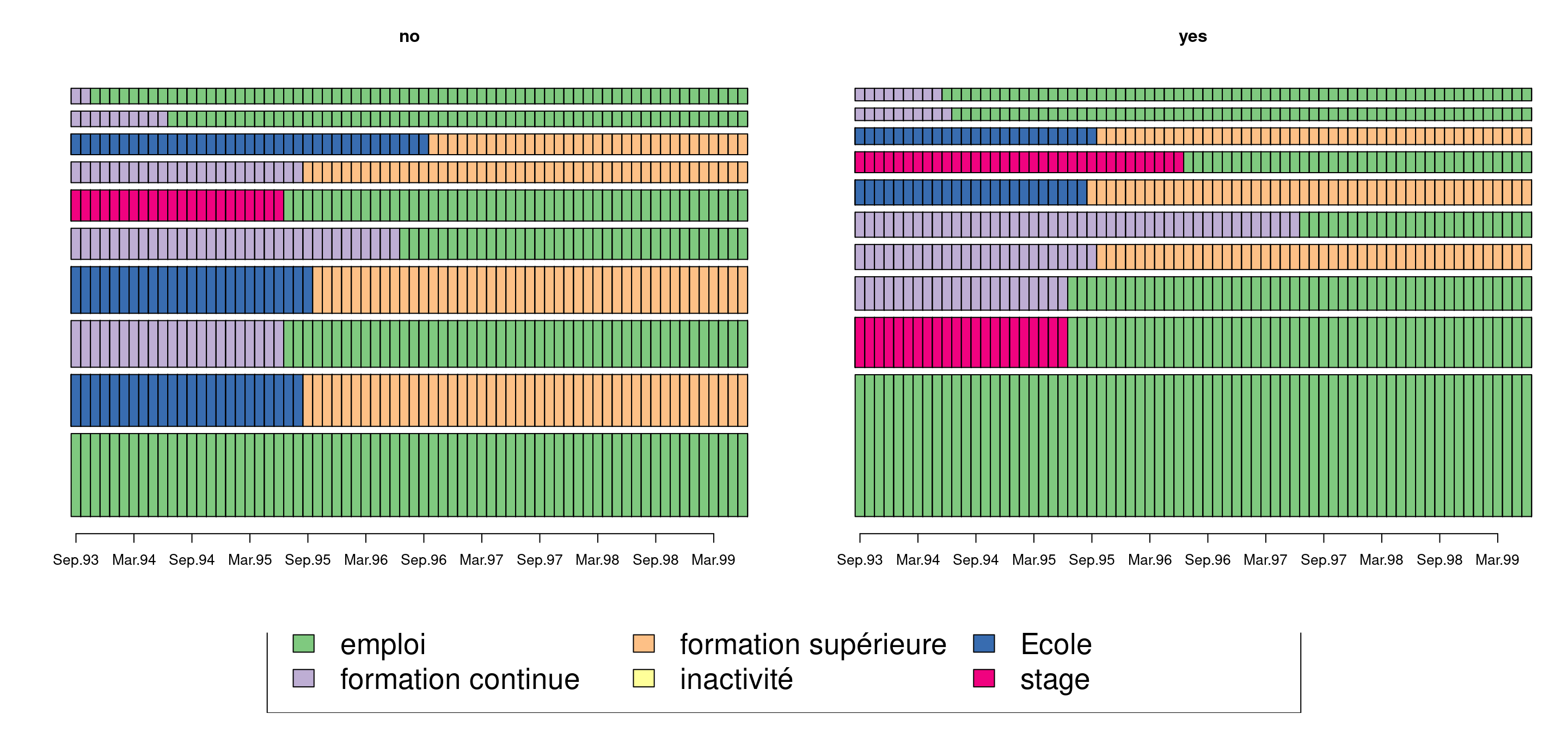
Ce graphique confirme les observations précédentes, les hommes durent plus longtemps dans les emplois que les femmes.
seqmsplot(mvad.seq, group = mvad$male, main = "classe", cex.legend = 2)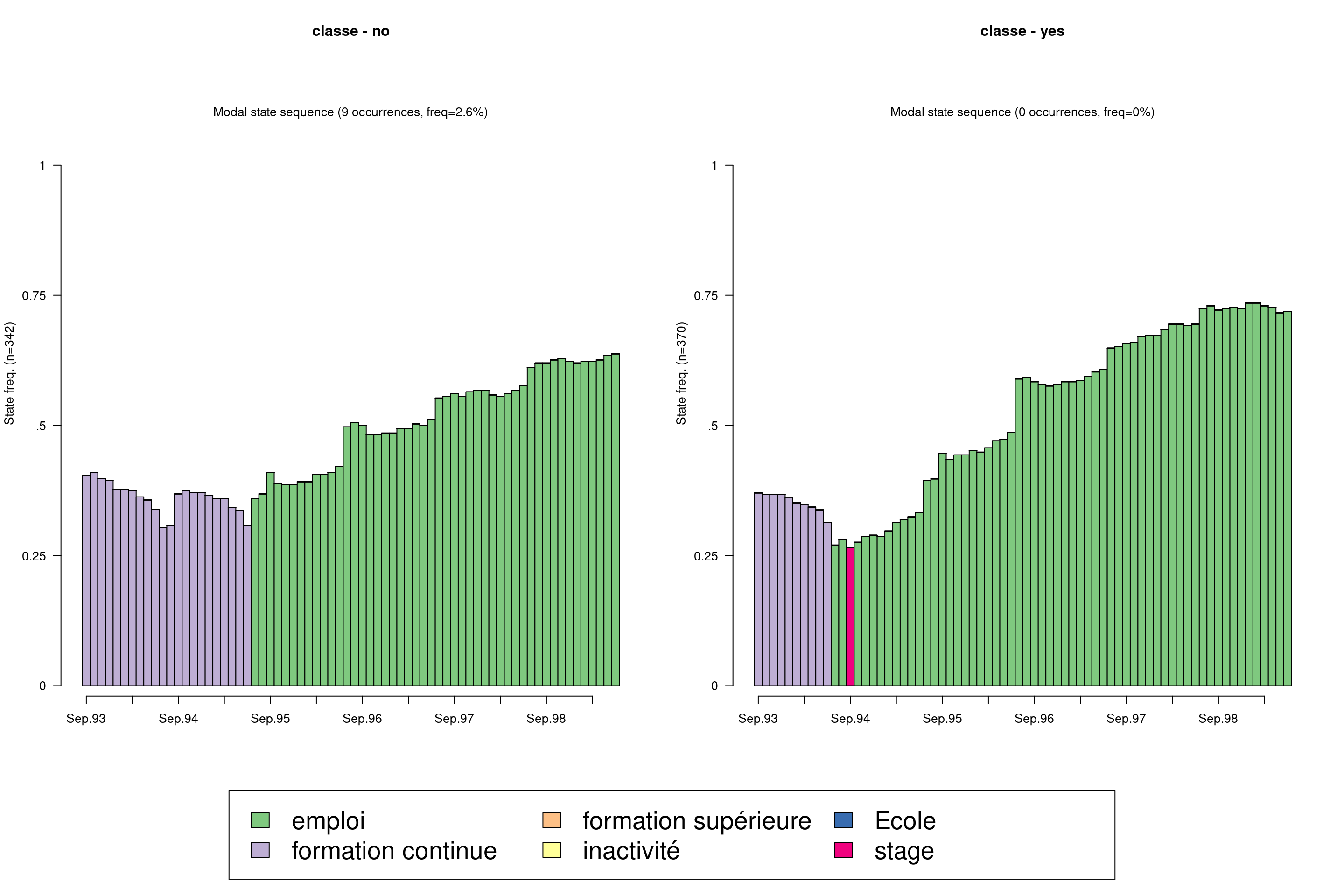
seqmtplot(mvad.seq, group = mvad$male, cex.legend = 2)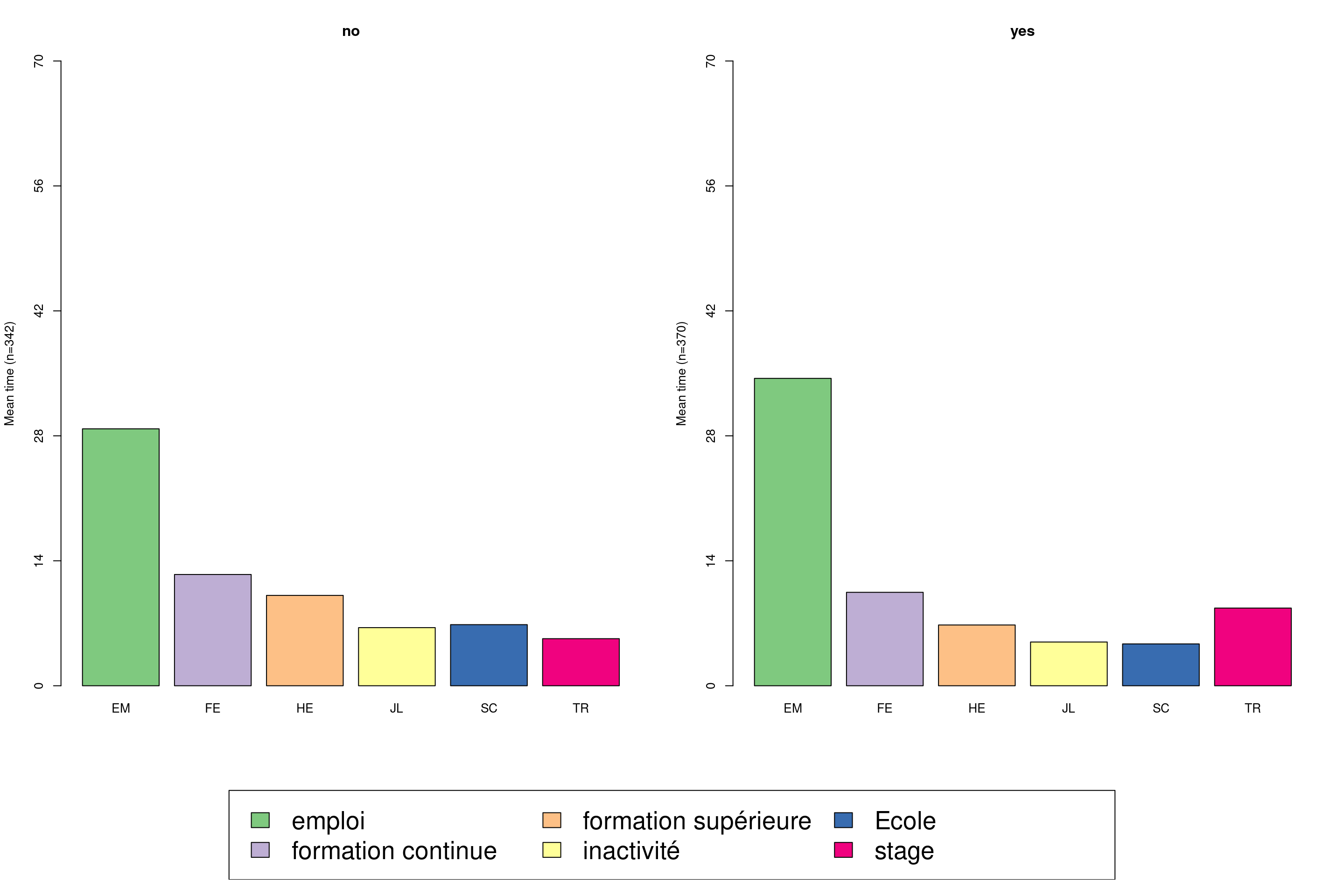
seqHtplot(mvad.seq, group = mvad$male)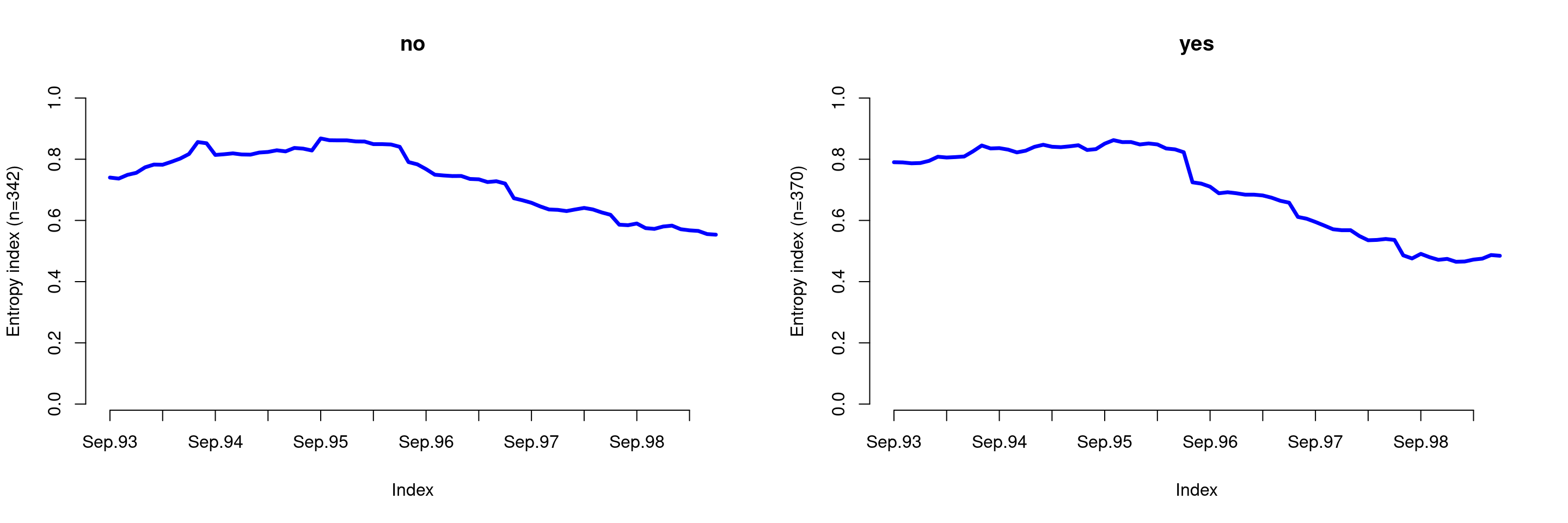
On remarque avec les entropies transversales que durant la période d’étude que ce soit chez les femmes ou chez hommes, les individus sont presque dispersés dans tous les états (entropie pas proche de 0).
Séquences d’événements
L’objectif ici est de considérer nos données comme une séquences d’événements et de déceler s’il y a :
- une configurations de types d’événements
- Relation avec covariables
- Quelle configuration caractérise le mieux un groupe par rapport aux autres ?
- Différences typiques dans les classes dans l’ordonnancement des événements
Tout d’abord, nous devons convertir notre objet d’état mvad.seq en séquence d’événements avec la fonction seqecreate
mvad.seqe <- seqecreate(mvad.seq, use.labels = FALSE)
head(mvad.seqe)## [1] (EM)-4-(EM>TR)-2-(TR>EM)-64
## [2] (FE)-36-(FE>HE)-34
## [3] (TR)-24-(TR>FE)-34-(FE>EM)-10-(EM>JL)-2
## [4] (TR)-47-(TR>EM)-14-(EM>JL)-9
## [5] (FE)-25-(FE>HE)-45
## [6] (JL)-1-(JL>TR)-33-(TR>EM)-36Comme nous pouvons le voir, l’objet mvad.seqe comprend des délais et des transitions.
Nous commençons par rechercher des sous-séquences d’événements fréquentes. Une sous-séquence est formée par un sous-ensemble des événements et qui respecte l’ordre des événements dans l’ordre. Par exemple, (EM>TR) -> (EM) est une sous-séquence de (EM>TR) -> (TR>HE) -> (EM) puisque l’ordre des événements sont respectés. Une sous-séquence est appelée « fréquente » si elle se produit dans plus d’un nombre minimum donné de séquences. Cela exigeait un nombre minimum de séquences auxquelles la sous-séquence doit appartenir et appelé support minimum. Le support minimum doit être fixé et peut être défini en pourcentages avec l’argument pMinSupport et en nombre par l’argument minSupport
fsubseq <- seqefsub(mvad.seqe, pmin.support = 0.05)
plot(fsubseq[1:15], col = "cyan", ylab="Fréquence", xlab="Sous-séquences", cex=0.7)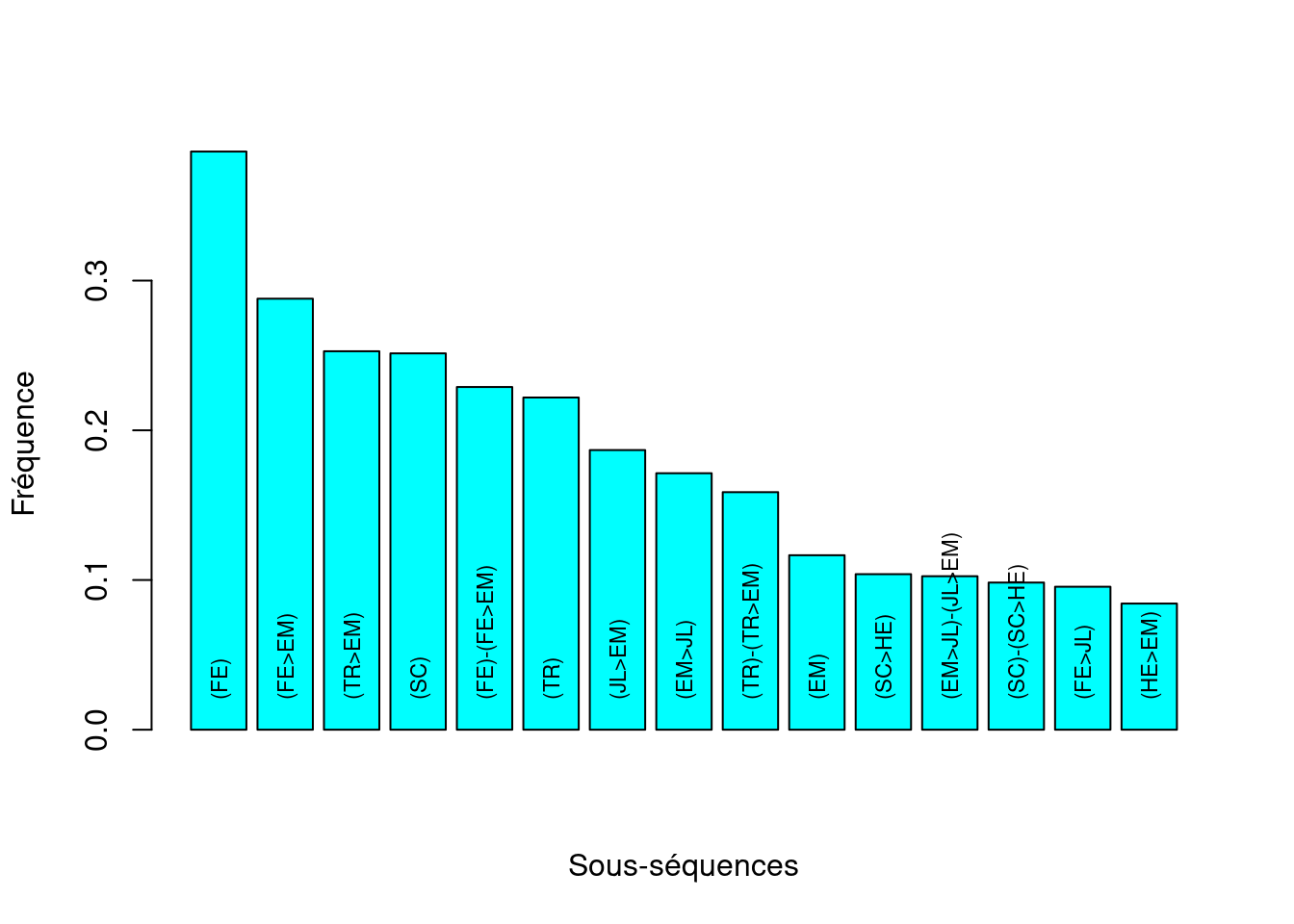
Cherchons les sous-séquences fréquentes liées au sexe. Notons que le pouvoir discriminant est évalué avec la p-value d’un test d’indépendance Khi-deux.
discr <- seqecmpgroup(fsubseq, group = mvad$male)
head(discr)## Subsequence Support p.value statistic index Freq.no Freq.yes
## 1 (SC) 0.25140449 0.0003881373 12.588453 4 0.31286550 0.19459459
## 2 (TR>EM) 0.25280899 0.0019363751 9.608891 3 0.19883041 0.30270270
## 3 (EM>FE) 0.05477528 0.0038514261 8.352568 27 0.08187135 0.02972973
## 4 (TR)-(TR>EM) 0.15870787 0.0046779765 7.999907 9 0.11695906 0.19729730
## 5 (TR) 0.22191011 0.0093698881 6.750929 6 0.17836257 0.26216216
## 6 (EM) 0.11657303 0.0153734703 5.873156 10 0.08479532 0.14594595
## Resid.no Resid.yes
## 1 2.266868 -2.179407
## 2 -1.985355 1.908756
## 3 2.141051 -2.058444
## 4 -1.938018 1.863245
## 5 -1.709575 1.643616
## 6 -1.721221 1.654813
##
## Computed on 712 event sequences
## Constraint Value
## count.method COBJplot(discr[1:6])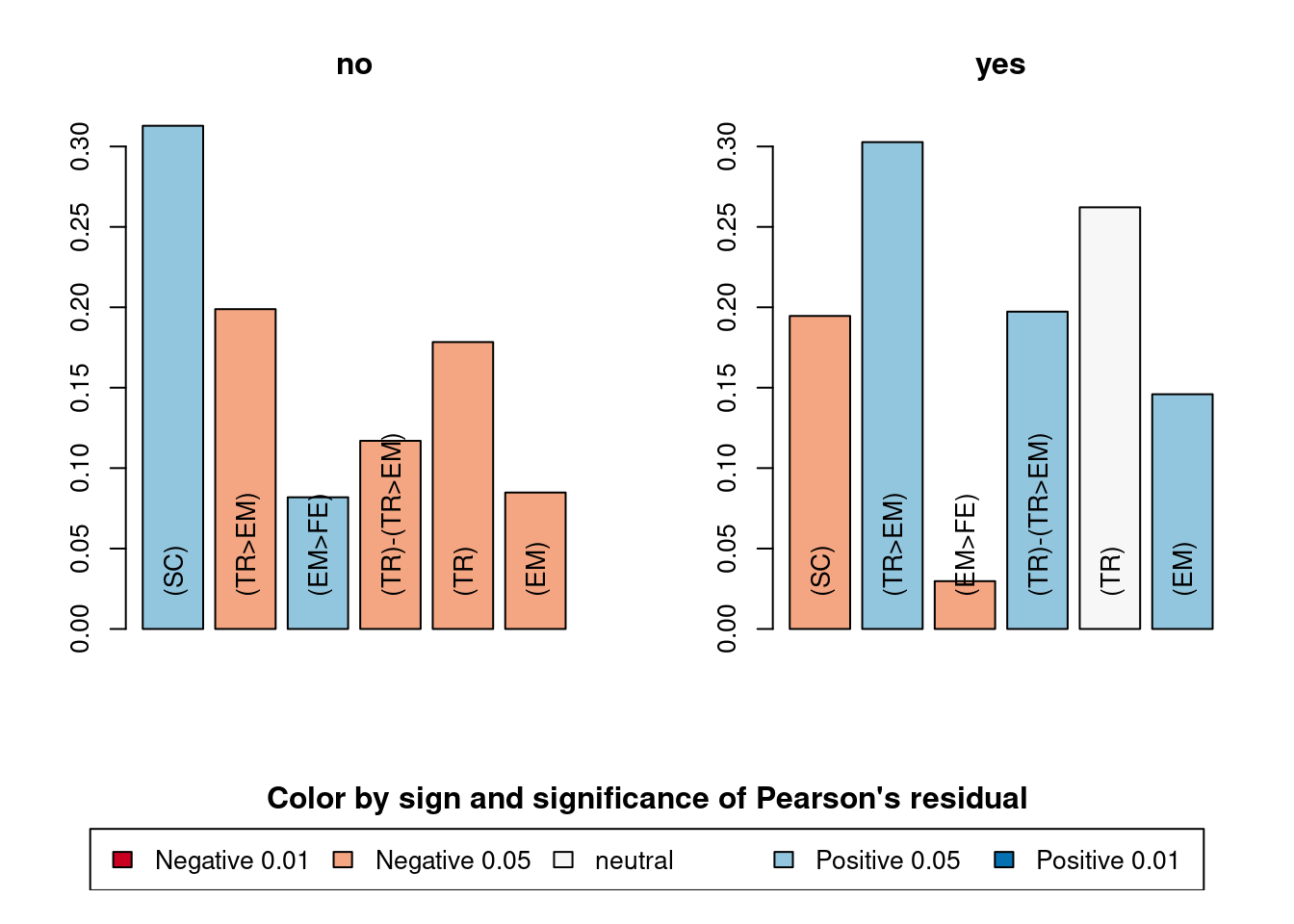
Règles d’association des séquences
rules <- TraMineR:::seqerules(fsubseq)
rules[,1:4]## Rules Support Conf Lift
## 1 (FE) => (FE>EM) 163 0.5927273 2.0586430
## 2 (TR) => (TR>EM) 113 0.7151899 2.8289733
## 3 (EM>JL) => (JL>EM) 73 0.5983607 3.2032540
## 4 (SC) => (SC>HE) 70 0.3910615 3.7626453
## 5 (FE) => (FE>JL) 52 0.1890909 1.9798930
## 6 (FE) => (JL>EM) 52 0.1890909 1.0122761
## 7 (SC) => (SC>EM) 50 0.2793296 3.5514765
## 8 (JL>EM) => (EM>JL) 45 0.3383459 1.9746087
## 9 (FE) => (FE>HE) 43 0.1563636 2.0616835
## 10 (TR) => (TR>JL) 42 0.2658228 3.2078953
## 11 (TR) => (JL>EM) 38 0.2405063 1.2875226
## 12 (FE) => (EM>JL) 37 0.1345455 0.7852161
## 13 (TR>EM) => (EM>JL) 37 0.2055556 1.1996357
## 14 (FE) => (TR>EM) 36 0.1309091 0.5178182La fonction renvoie des règles d’association séquentielles. L’apprentissage des règles d’association utilise une valeur de support minimal comme paramètre principal.
Nous obtenons des règles au format si/alors avec plusieurs statistiques. Par exemple, le premier
(FE) => (FE>EM) signifie: si un individu qui a suivi une formation continue (FE) est susceptible de trouver un emploi (EM). Cette règle a 168 supports (c’est-à-dire qu’elle est appliquée en 163 séquences). La confiance 0.5927273 signifie que dans 59,27%, un individu qui a suivi une formation continue a trouvé un emploi.
Conclusion
Ainsi, sommes arrivé à la fin de ce tutoriel destiné à l’analyse et visualisation séquentielle sociale.
Pour écrire ce tutoriel, je me suis inspéré de l’article “L’analyse de séquences” de Nicolas Robette.
j’espère que ça permettra au plus grand nombre d’analyser et visualiser leur donnée de séquences.
Si quelque chose vous freine ou vous pose problème dans les codes, indiquez le moi en commentaire, et j’essaierais de vous apporter une réponse.
Si cet tutoriel vous a plu ou vous a été utile, n’oubliez pas de le partager !.
References
Robette, Nicolas, and Nicolas Thibault. 2008. “Analyse Harmonique Qualitative Ou Méthodes d’appariement Optimal?” Population 63 (4): 621–46.
Studer, Matthias. 2013. “WeightedCluster Library Manual: A practical guide to creating typologies of trajectories in the social sciences with R.” LIVES Working Papers 24.
Studer, Matthias, and Gilbert Ritschard. 2016. “What matters in differences between life trajectories: a comparative review of sequence dissimilarity measures.” Journal of the Royal Statistical Society, Series A 179 (2): 481–511. https://doi.org/10.1111/rssa.12125.
