 Source: Data Mining Concepts and Techniques, Third Edition.
Source: Data Mining Concepts and Techniques, Third Edition.
Introduction
Le concept de l’analyse du panier de la ménagère fait référence à une technique d’analyse de données utilisée pour comprendre les comportements des clients, en fonction de leur similitude au produits qu’ils achètent et pour découvrir les relations entre ces produits achetés. L’idée serait pour une entreprise d’utiliser ces apprentissages pour bien mener les campagnes marketing, mieux gérer les inventaires, aider les clients à trouver plus rapidement des produits pertinents et améliorer les relations clients. Cela peut conduire à davantage de ventes croisées et de ventes incitatives en suggérant des produits ou services supplémentaires.
Dans ce tutoriel, nous allons voir comment nous pouvons analyser et visualiser les données de transactions, nous trouverons des techniques qui peuvent nous aider à trouver des modèles de comportement et de désabonnement d’un client en fonction de sa séquence d’achat. Ce tutoriel est basé sur l’article de Suman ghorai intitulé “Market Basket Analysis”.

Quelques notions de bases
Règles de l’Association
Le but de l’analyse du panier de la ménagère est souvent d’identifier les règles d’association entre les articles et cela peut être fait par l’algorithme Apriori. Une règle d’association implique que si un élément A se produit, alors l’élément B se produit également avec une certaine probabilité. A titre d’exemple, considérons l’exemple suivant:
| transaction | articles |
|---|---|
| T1 | {pain, lait, sucre} |
| T2 | {pain, œufs} |
| T3 | {œufs, Mayonnaise} |
| T4 | {pain, lait, œufs} |
| T5 | {pain, lait, Couches, œufs, sucre} |
| T6 | {lait, Couches, sucre} |
| T7 | {lait, sucre, Couches} |
Dans le tableau ci-dessus, nous pouvons voir sept transactions. Chaque transaction montre les articles achetés dans cette transaction. Nous pouvons représenter nos articles comme un ensemble d’éléments comme suit :
\[ I = \{i_1, i_2, \cdots, i_k\} \] Où \(k\) est le nombre total d’articles.
Dans le cas de notre table ci-dessus, nous avons
\[ I = \{ \mbox{pain, lait, sucre, œufs, Mayonnaise, Couches} \}\]
Et l’ensemble des transactions est :
\[T = \{ T_1, T_2, T_3, T_4, T_5, T_6, \cdots, T_N \}\] où \(N\) est le nombre total de transactions.
Par exemple dans notre cas on a:
\[ T_1 = \{\mbox{pain, lait, sucre}\} \]
Ensuite, la règle d’association est définie comme une implication de la forme :
\[ X \Rightarrow Y,\,\, \mbox{où}\,\, X\subset I, Y\subset I\,\, \mbox{et}\,\, X\cap Y = \emptyset \]
Par exemple, on peut extraire de notre table ci-dessus, la règle suivante:
\[\{\mbox{pain, lait}\} \Rightarrow \{\mbox{sucre}\} \]
Toutefois, on peut se poser la question de savoir jusqu’à quel niveau cette règle est elle plausible ? ou encore comment évaluer cette règle?
Dans la section suivante, nous allons définir quatre mesures qui nous permettrons d’évaluer la précision d’une règle d’association.
Mésures d’évaluation
Support
Le support est une indication de la fréquence d’apparition de l’ensemble des items du panier dans l’ensemble de données. Il représente la fiabilité. Ce critère permet de fixer un seuil en dessous duquel les règles ne sont pas considérées comme fiables. Il est défini comme suit:
\[supp(X\Rightarrow Y)=\frac{|X \cup Y| }{N}\] En d’autres termes, c’est le nombre de transactions avec les deux \(X\) et \(Y\) divisé par le nombre total de transactions. Par exemple avec notre table ci-dessus, nous avons:
\(supp(\mbox{pain} \Rightarrow \mbox{lait}) = \frac{3}{7} = 43\%\)
\(supp(\mbox{pain} \Rightarrow \mbox{sucre}) = \frac{2}{7} = 29\%\)
La confiance
La confiance est une indication de la précision de la règle. Pour une règle \(X\Rightarrow Y\), cela signifie pour \(X\) donné quelle est la probabilité d’avoir \(Y\) dans la même transaction? La confiance d’une règle peut être vue comme la probabilité conditionnelle \(conf(X\Rightarrow Y) = Pr(Y|X)\).
\[conf(X\Rightarrow Y) = \frac{supp(X\cup Y)}{supp(X)}\]
Exemple avec notre table de transactions ci-dessus:
- Considérons la règle \(\{\mbox{pain, lait}\} \Rightarrow \{\mbox{œufs}\}\), le support de l’ensemble \(\{\mbox{pain, lait}, \mbox{œufs}\}\) est \(2\) et le nombre de transaction étant \(7\), le support de la règle est donc \(2/7\). La confiance est obtenue en divisant le support de l’ensemble \(\{\mbox{pain, lait}, \mbox{œufs}\}\) par le support de l’ensemble \(\{\mbox{pain, lait}\}\) qui est égal à \(4\). La confiance est donc égale à \(2/4 = 50\%\).
\[conf(\{\mbox{pain, lait}\} \Rightarrow \{\mbox{œufs}\}) = \frac{2/7}{4/7} = 50\%\]
- \(conf(\mbox{lait} \Rightarrow \mbox{sucre}) = \frac{4/7}{5/7} = 80\%\)
Lift
Le lift d’une règle est le rapport du support observé et du support attendu si \(X\) et \(Y\) étaient indépendant. Il est défini comme suit:
\[lift(X \Rightarrow Y)= \frac{supp(X\cup Y)}{supp(X)supp(Y)}\] Un lift supérieur à \(1\) indique qu’il existe bien un lien entre les \(2\) éléments.
- \(lift(\mbox{lait} \Rightarrow \mbox{sucre}) = \frac{4/7}{(5/7)(4/7)} = 1.4\)
Description des données
L’ensemble de données comprend 21293 observations provenant d’une boulangerie. Le fichier de données contient quatre variables, date, heure, Numéro d’identification des transactions et articles. Numéro d’identification des transactions va de 1 à 9684.
Les données sont disponible ici.
Chargement des packages
Commençons donc par charger les librairies dont nous avons besoins et notre ensemble de données.
library(googleVis)
library(tidyverse)
library(lubridate)
library(kableExtra)
library(arules)
library(gridExtra)
library(arulesViz)
trans <- read.transactions("BreadBasket_DMS.csv"
, format = "single", cols = c(3,4)
, sep = ",", rm.duplicates = TRUE)Analayse et visualisation des donnnées
Dans un premier temps, traçons la fréquence d’achat des articles, afin
d’avoir une idée sur la distribution des produits. Nous utilisons la fonction
itemFrequencyPlot().
itemFrequencyPlot(trans, topN = 20, type = "absolute"
, col = "wheat2", xlab = "Achat"
, ylab = "Frequence"
, main = "Frenquence d'achat des produits")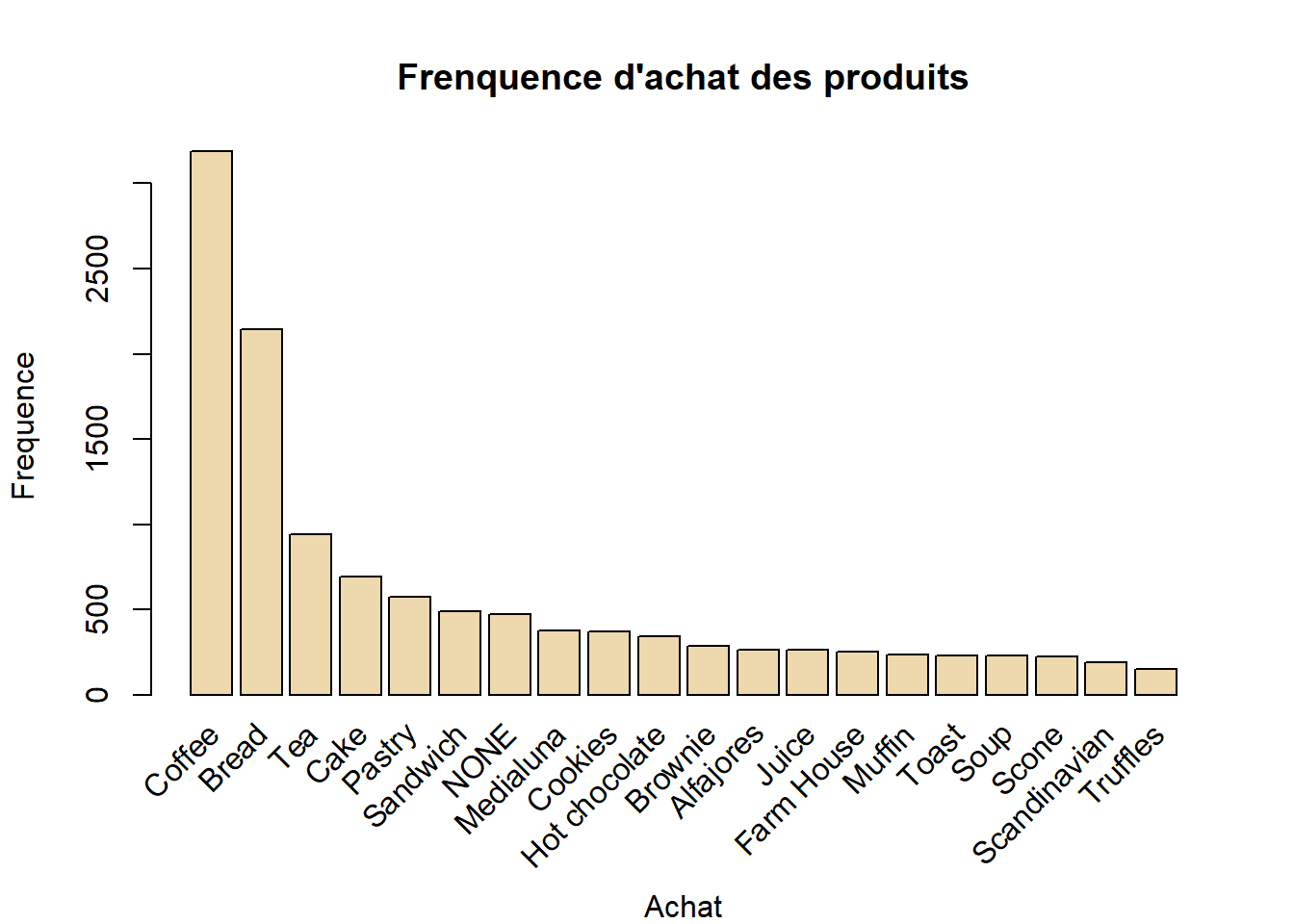
Le café (coffee) est de loin le produit le plus vendu, suivi du pain (bread). Il est aussi possible de visualiser les transactions en foncton des dates.
Nombre de transactions par mois
trans_csv <- read.csv("BreadBasket_DMS.csv")
trans_csv %>%
mutate(Date = as.Date(Date, format = "%Y-%m-%d")) %>%
mutate(Month = as.factor((lubridate::month(Date, label = TRUE)))) %>%
group_by(Month) %>%
summarise(Transactions = n_distinct(Item)) %>%
ggplot(aes(x = Month, y = Transactions)) +
geom_bar(stat = "identity", fill = "mistyrose2", show.legend = TRUE, colour = "black") +
geom_label(aes(label = Transactions)) +
ggtitle("Transactions par Mois") +
xlab("Mois") +
theme(plot.title = element_text(hjust = 1)) +
ggeasy::easy_center_title() +
theme_bw()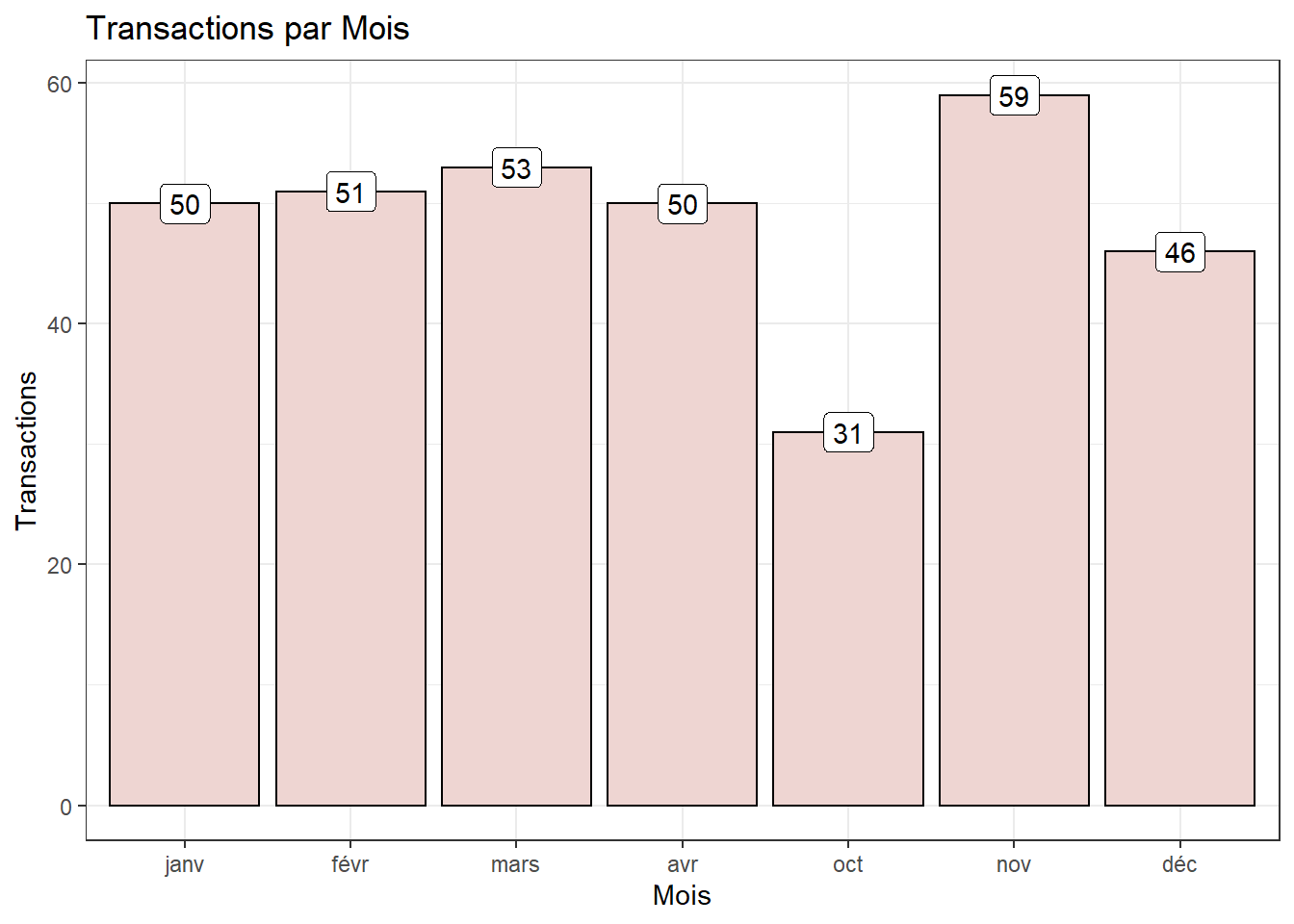
Les données couvrent les dates du 30/10/2016 au 09/04/2017 et donc le mois d’octobre est le mois dont nous avons peu de transactions par rapport aux autres mois.
Nombre de transactions par jour de la Semaine
trans_csv %>%
mutate(Date = as.Date(trans_csv$Date, format = "%Y-%m-%d")) %>%
mutate(WeekDay = as.factor(weekdays(Date))) %>%
group_by(WeekDay) %>%
summarise(Transactions = n_distinct(Item)) %>%
ggplot(aes(x = WeekDay, y = Transactions)) +
geom_bar(stat = "identity", fill = "peachpuff2",
show.legend = FALSE, colour = "black") +
geom_label(aes(label = Transactions)) +
labs(title = "Transactions par jour de la semaine") +
xlab("Jours de la semaine") +
scale_x_discrete(limits = c("lundi", "mardi", "mercredi", "jeudi",
"vendredi", "samedi", "dimanche")) +
theme_bw() 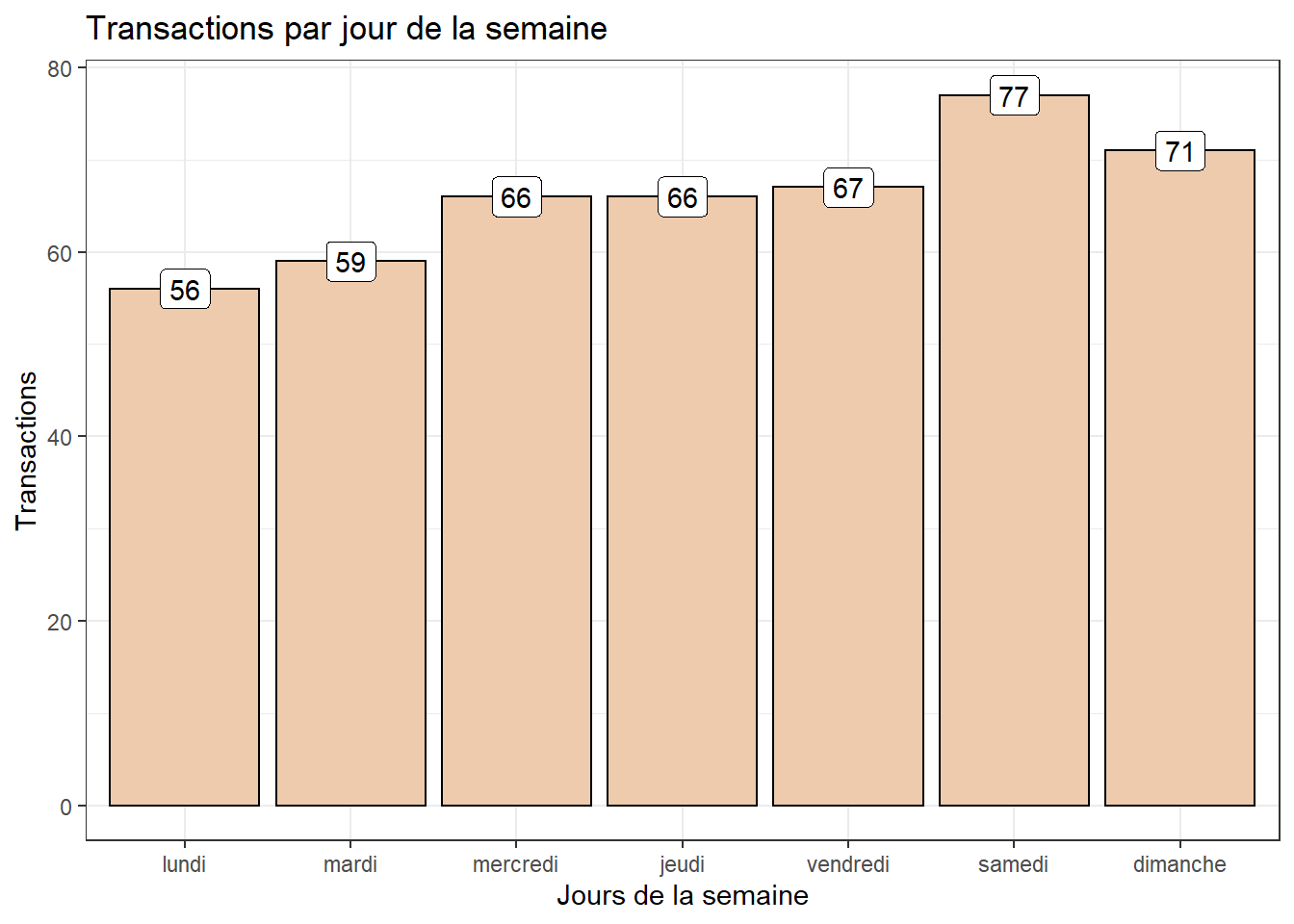
Comme on peut le voir clairement qu’en général, il y a des achats dans l’épicerie tous les jours de la semaine avec un taux moins élevé les lundi et mardi.
Nombre de transactions par heure
trans_csv %>%
mutate(Hour = as.factor(hour(hms(Time)))) %>%
group_by(Hour) %>%
summarise(Transactions = n_distinct(Transaction)) %>%
ggplot(aes(x = Hour, y = Transactions)) +
geom_bar(stat="identity", fill = "steelblue1"
, show.legend = FALSE, colour = "black") +
geom_label(aes(label = Transactions)) +
labs(title = "Transactions par heure") +
xlab("Heure") + ylab("Nombre de transactions") +
theme_bw()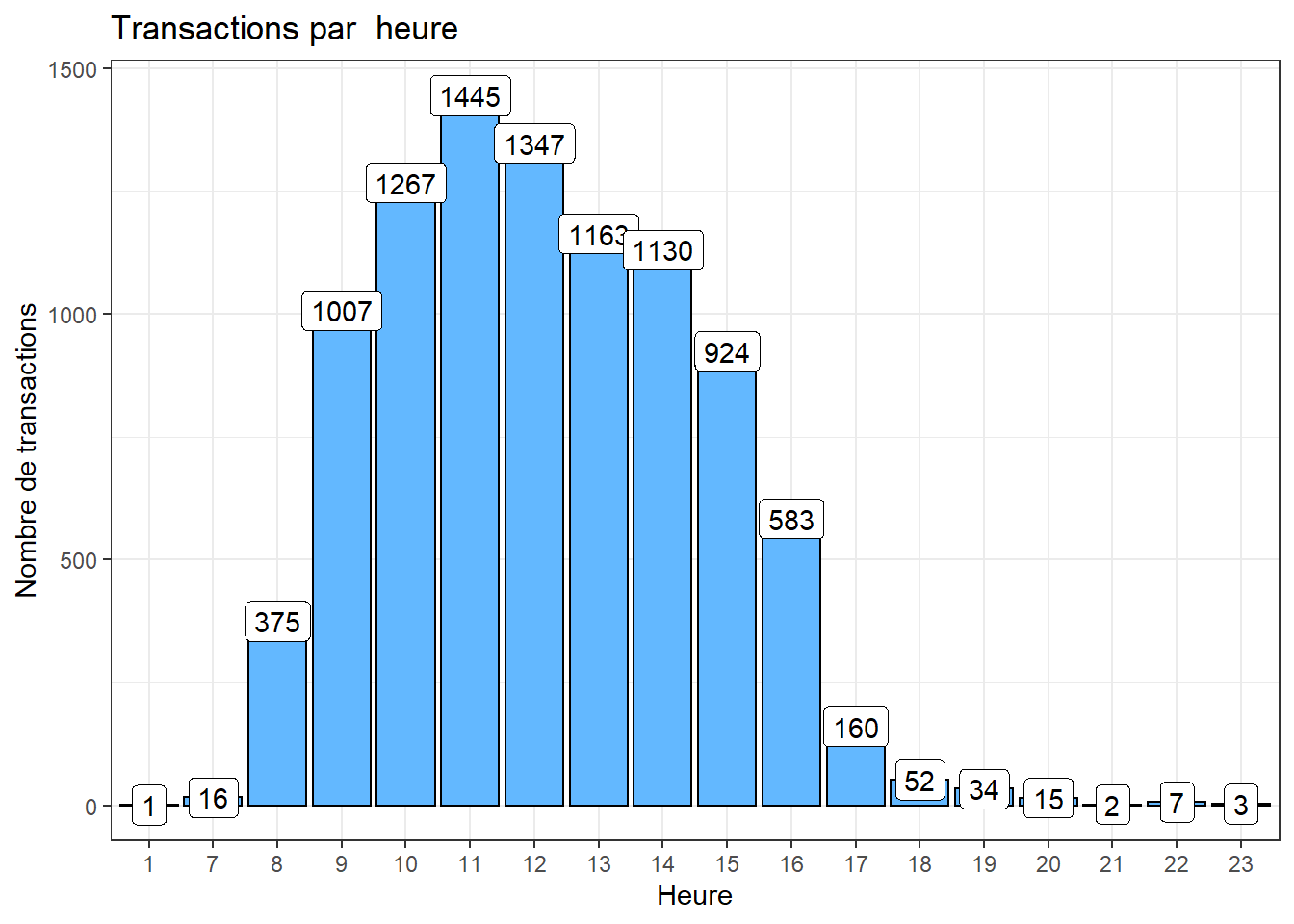
On a plus de transactions à 11h dans la boulangerie.
Algorithme apriori
Choix du support et de la confiance
Le choix d’un seuil pour le support et la confiance est important dans la détermination des règles d’association. Pour des valeurs trop bas, l’algorithme prend plus de temps à exécuter et beaucoup de règles sont détecter (la plupart d’entre elles ne sont pas utiles). Alors, quelles valeurs choisies? Il est recommandé de tester plusieurs valeurs et voir graphiquement combien de règles sont générées pour chaque combinaison.
# Différentes valeurs du support et de la confiance
supportLevels <- c(0.1, 0.05, 0.01, 0.005)
confidenceLevels <- c(0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1)
rules_sup10 <- integer(length = 9)
rules_sup5 <- integer(length = 9)
rules_sup1 <- integer(length = 9)
rules_sup0.5 <- integer(length = 9)
# L'algorithme Apriori avec un support de 0.1
for (i in 1:length(confidenceLevels)) {
rules_sup10[i] <- length(apriori(trans, parameter = list(sup = supportLevels[1],
conf = confidenceLevels[i], target = "rules")))
}
# L'algorithme Apriori avec un support de 0.5
for (i in 1:length(confidenceLevels)){
rules_sup5[i] <- length(apriori(trans, parameter=list(sup = supportLevels[2],
conf = confidenceLevels[i], target = "rules")))
}
# L'algorithme Apriori avec un support de 0.01
for (i in 1:length(confidenceLevels)){
rules_sup1[i] <- length(apriori(trans, parameter = list(sup = supportLevels[3],
conf=confidenceLevels[i], target = "rules")))
}
# L'algorithme Apriori avec un support de 0.005
for (i in 1:length(confidenceLevels)){
rules_sup0.5[i] <- length(apriori(trans, parameter = list(sup = supportLevels[4],
conf = confidenceLevels[i], target = "rules")))
}Dans la figure suivante, nous avons le nombre de règles générées avec différentes valeurs du support et de la confiance.
num_rules <- data.frame(rules_sup10, rules_sup5, rules_sup1, rules_sup0.5, confidenceLevels)
# Nombre de règles avec support : 0.1, 0.05, 0.01, 0.005
ggplot(data = num_rules, aes(x = confidenceLevels)) +
geom_line(aes(y = rules_sup10, colour = "Support de 0.1")) +
geom_point(aes(y = rules_sup10, colour = "Support de 0.1")) +
geom_line(aes(y = rules_sup5, colour = "Support de 0.05")) +
geom_point(aes(y = rules_sup5, colour = "Support de 0.05")) +
geom_line(aes(y = rules_sup1, colour = "Support de 0.01")) +
geom_point(aes(y = rules_sup1, colour = "Support de 0.01")) +
geom_line(aes(y = rules_sup0.5, colour = "Support de 0.005")) +
geom_point(aes(y = rules_sup0.5, colour = "Support de 0.05")) +
labs( x = "Niveau de confiance", y = "Nombre de règles",
title = "Algorithme Apriori avec différentes valeurs du support") +
theme_bw() +
theme(legend.title = element_blank())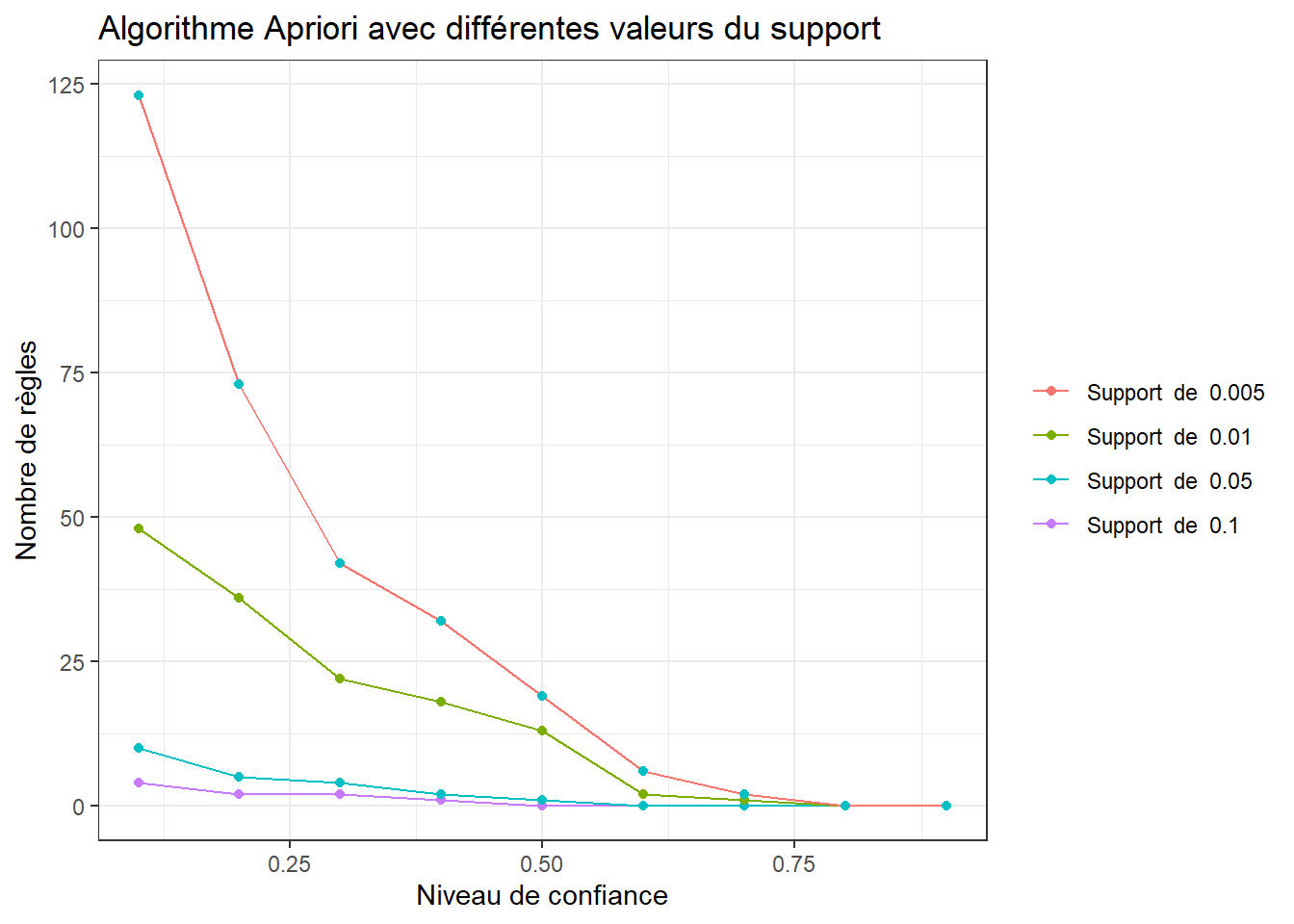
Analysons le graphique:
Avec un support de 0.1, nous avons que quelques règles avec une confiance très faible. Cela signifie qu’il n’y a pas assez d’associations fréquentes dans notre ensemble de données. Les règles qui en résultent ne sont donc pas représentatives.
Avec un support de 0.05, nous obtenons une règle avec une confiance inférieure à 0.5.
Pour un support de 0.01, nous obtenons des règles dont au moins 13 ont une confiance de d’au moins de 0.5.
Pour une confiance de 0.005, trop de règles à analyser.
Pour résumer, nous allons utiliser un support de 0.01 et un confiance de 0.5.
rules_sup1_conf50 <- apriori(trans, parameter = list(sup = supportLevels[3],
conf = confidenceLevels[5], target = "rules"))
# Inspection des règles d'association
inspect(rules_sup1_conf50)## lhs rhs support confidence coverage lift
## [1] {Tiffin} => {Coffee} 0.01058361 0.5468750 0.01935289 1.134577
## [2] {Spanish Brunch} => {Coffee} 0.01406108 0.6326531 0.02222558 1.312537
## [3] {Scone} => {Coffee} 0.01844572 0.5422222 0.03401875 1.124924
## [4] {Toast} => {Coffee} 0.02570305 0.7296137 0.03522830 1.513697
## [5] {Alfajores} => {Coffee} 0.02237678 0.5522388 0.04052011 1.145705
## [6] {Juice} => {Coffee} 0.02131842 0.5300752 0.04021772 1.099723
## [7] {Hot chocolate} => {Coffee} 0.02721500 0.5263158 0.05170850 1.091924
## [8] {Medialuna} => {Coffee} 0.03296039 0.5751979 0.05730269 1.193337
## [9] {Cookies} => {Coffee} 0.02978530 0.5267380 0.05654672 1.092800
## [10] {NONE} => {Coffee} 0.04172966 0.5810526 0.07181736 1.205484
## [11] {Sandwich} => {Coffee} 0.04233444 0.5679513 0.07453886 1.178303
## [12] {Pastry} => {Coffee} 0.04868461 0.5590278 0.08708800 1.159790
## [13] {Cake} => {Coffee} 0.05654672 0.5389049 0.10492894 1.118042
## count
## [1] 70
## [2] 93
## [3] 122
## [4] 170
## [5] 148
## [6] 141
## [7] 180
## [8] 218
## [9] 197
## [10] 276
## [11] 280
## [12] 322
## [13] 374Interprétation des règles
54% des clients qui ont acheté un Tiffin chaud ont également acheté un café.
63% des clients qui ont acheté un Spanish Brunch ont également acheté un café.
73% des clients qui ont acheté un toast ont également acheté un café.
Et ainsi de suite. Il semble que dans cette boutique, il y ait beaucoup d’amoureux du café.
Visualiser les règles d’association
Visualisons quelques graphiques des règles avec la libraire arulesViz.
Commençons par un simple nuage de points avec les différentes mesures
d’intérêt sur les axes (lift et support) et confiance représentée par la
couleur des points.
plot(rules_sup1_conf50, measure = c("support", "lift")
, shading = "confidence", main = "Nuage de points des mesures")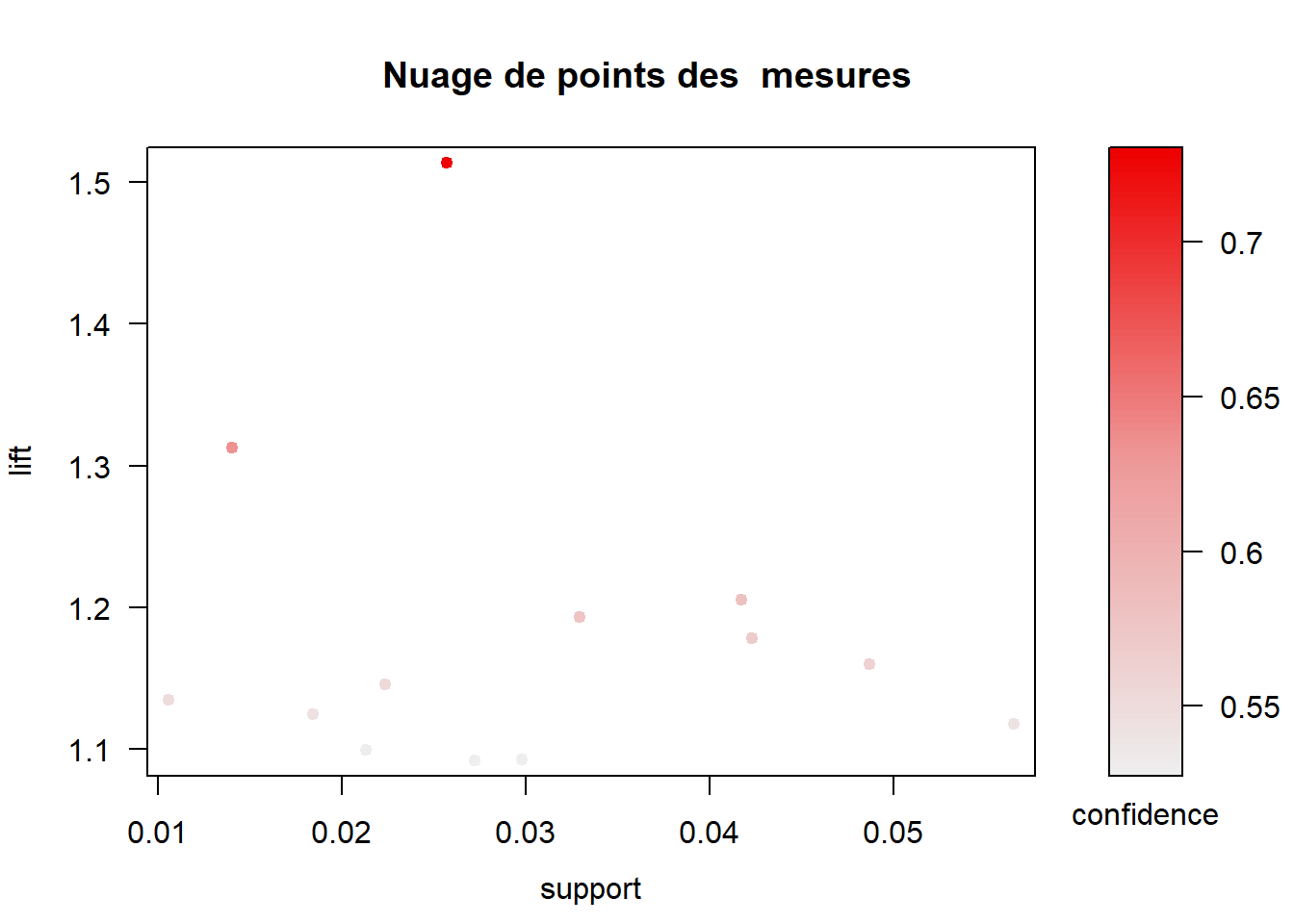
Le graphique suivant représente le graphe des règles d’association. Les sommets représentent les articles et les règles sont représentées par les liaisons entre les articles à l’aide de flèches.
plot(rules_sup1_conf50, method = "graph", control = list(layout=igraph::in_circle())
, main = "Graphe des règles d'association")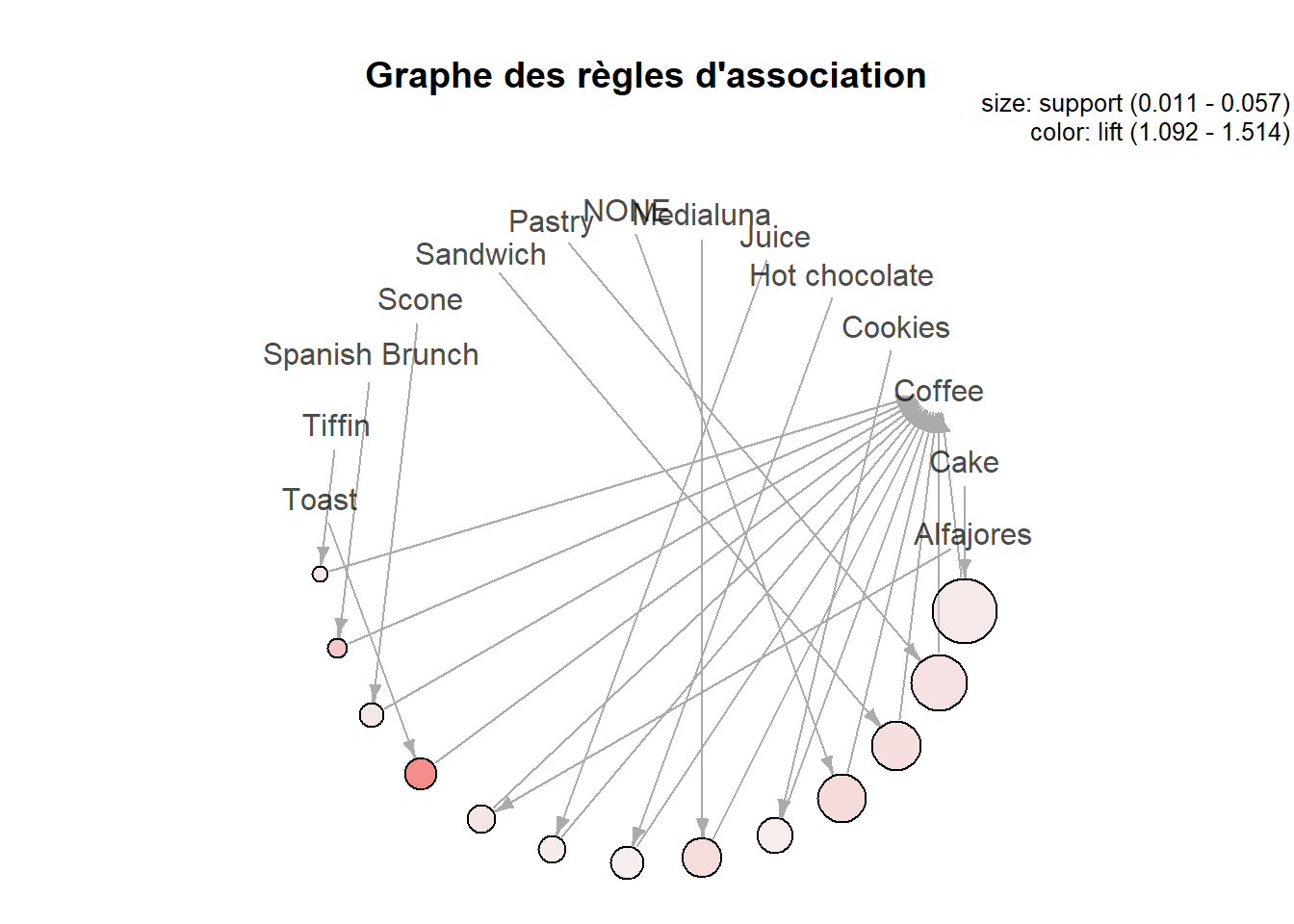
Il est aussi possible de représenter les règles sous une forme matricielle groupée. Le support et le lift sont représentés par la taille et la couleur des bulles respectueusement.
plot(rules_sup1_conf50, method = "grouped")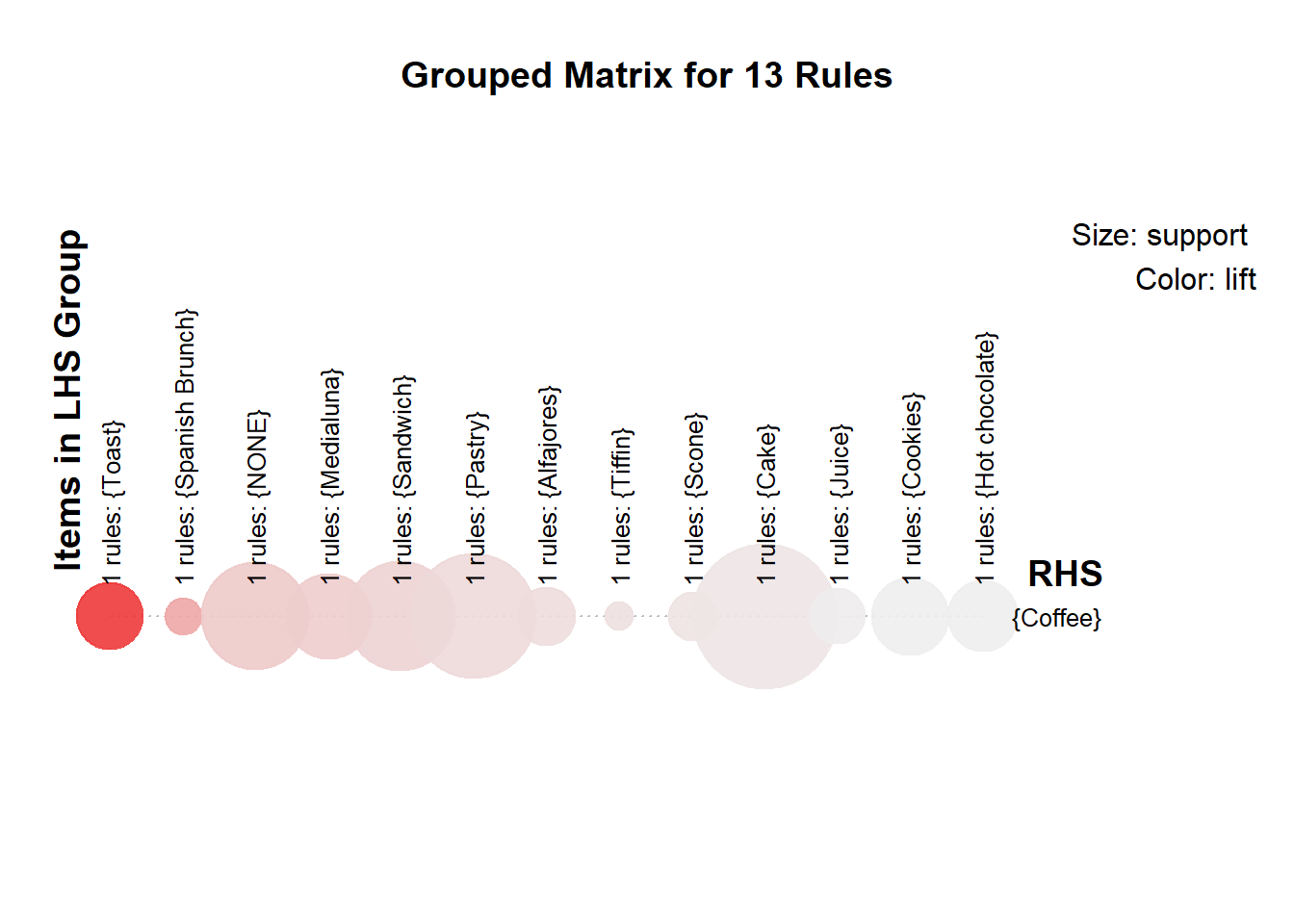
Conclusion
L’analyse du panier de la ménagère est une technique très utile pour analyser les données. Traditionnellement, il n’est utilisé que pour les données de transaction. Cela permettra de booster vos ventes et de garder une bonne relation avec vos clients. J’espère que cela vous aidera à faire votre propre analyse des transactions et à bien disposer les articles qui sont liés entre eux.
Si quelque chose vous freine ou vous pose problème dans les codes, indiquez le moi en commentaire, et j’essaierais de vous apporter une réponse.
Si cet tutoriel vous a plu ou vous a été utile, n’oubliez pas de le partager !.
